Квадратне рівняння

Квадратне рівняння — це рівняння вигляду

a x² + b x + c = 0,

де a не дорівнює 0.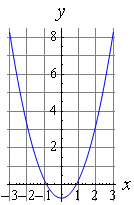

Геометричний зміст
Вивід формули для розв'язання квадратного рівняння
Дискримінант квадратного рівняння
Теорема Вієта
Розклад квадратного рівняння на множники
Приклади розв'язання квадратних рівнянь

Геометричний зміст

Графіком квадратичної функції є парабола. Розв'язками (коренями) квадратного рівняння називають точки перетину параболи з віссю абсцис. Якщо парабола, яка описується квадратичною функцією, не перетинається з віссю абсцис, рівняння не має дійсних корнів. Якщо парабола перетинається з віссю абсцис в одній точці (вершині параболи), рівняння має один дійсний корінь (також кажуть, що рівняння має два співпадаючих кореня). Якщо парабола перетинає вісь абсцис в двох точках, рівняння має два дійсних кореня.

Якщо коефіцієнт a додатній, вітки параболи направлені вгору, якщо від'ємний — вітки параболи направлені вниз. Якщо коефіцієнт b додатній, то вершина параболи лежить в лівій півплощині, якщо від'ємний — в правій півплощині.

Вивід формули для розв'язання квадратного рівняння

Формулу для розв'язання квадратного рівняння a x² + b x + c = 0 можна отримати так:

перенесемо c в праву частину a x² + b x = - c
помножимо рівняння на 4a (2a x)² + 4a b x = - 4a c
додамо b² до обох частин (2a x)² + 4a b x + b² = b² - 4a c
в лівій частині виділимо повний квадрат (2a x + b)² = b² - 4a c
знайдемо квадратний корінь 2a x + b = ± √b² - 4a c
перенесемо b в праву частину 2a x = - b ± √b² - 4a c
розділимо рівняння на 2a

x = -b ± √b² - 4a c
2 a

Дискримінант квадратного рівняння

Дискримінантом

квадратного рівняння називають число яке дорівнює D = b² − 4ac

Квадратне рівняння з дійсними коефіцієнтами може мати від 0 до 2 дійсних коренів в залежності від значення дискримінанта:

коли D > 0 корнів два, и вони обчислюються за формулою
x_1,2 = -b ± √D
2 a
коли D = 0 корінь один (два рівних або співпадаючих коріня), кратності 2:
x = -b
2 a
коли D < 0 дійсних коренів нема. Існують два комплексних кореня, які можна знайти за формулою
x_1,2 = -b ± i√-D
2 a

Теорема Вієта

Зведеним квадратним рівнянням

називається рівняння, в якому коефіцієнт при x² дорівнює одиниці. Таке рівняння може бути отримане діленням всього виразу на коефіцієнт a: x² + px + q = 0, де p = ba, q = ca

Сума коренів зведеного квадратного рівняння

x² + px + q = 0 дорівнює коефіцієнту p, взятому з оберненим знаком, а добуток коренів дорівнює вільному члену q:
x₁ + x₂ = -p, x₁x₂ = q.

Розклад квадратного рівняння на множники

Якщо відомі обидва кореня квадратного рівняння, його можна розкласти за формулою

ax² + bx + c = a(x - x₁)(x - x₂)

Приклади розв'язання квадратних рівнянь

Наприклад. Знайти корені квадратного рівняння: 2x² + 5x + 3 = 0
D = 5² - 4·3·2 = 25 - 24 = 1

x₁ =	-5 + √1	= -1,
	2·2

x₂ =	-5 - √1	= -1	1
	2·2		2

Вправи. Квадратне рівняння

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!

x =	-b ± √b² - 4a c
	2 a

x_1,2 =	-b ± √D
	2 a

x_1,2 =	-b ± i√-D
	2 a