ЗНО онлайн 2015 року з математики (варіант 1)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Витрачено часу: 0

Вправа 1 з 30

Витрачено часу: 0

Вправа 1 з 30

2(5x + 6) =

Оберіть вірну відповідь:

А 10x + 12

Б 10x + 6

В 7x + 8

Г 7x + 12

Д 5x + 8

Для розв'язання цього прикладу достатньо розкрити дужки:

2·(5x + 6) = 2·5x + 2·6=10x + 12.

Тому треба обрати пункт "А".

На рисунку зображено рівнобедрений трикутник ABC (AB =BC). Визначте градусну міру кута BAC, якщо ∠B = 40°.

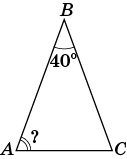
Оберіть вірну відповідь:

А 80°

Б 70°

В 60°

Г 50°

Д 40°

Сума кутів трикутника дорівнює 180°.

Кути при основі рівнобічного трикутника рівні ∠A = ∠C.

Тому ∠A + ∠B + ∠C = 180°

∠A + 40° + ∠A = 180°

2∠A = 180° - 40° = 140°

∠A = 140°/2 = 70°

Тому треба обрати пункт "Б".

Розв'яжіть нерівність 0,2x − 54 < 0.

Оберіть вірну відповідь:

А (−∞; 27)

Б (270; +∞)

В (−∞; 2,7)

Г (−∞; 270)

Д (10,8; +∞)

0,2x − 54 < 0

0,2x < 54

x < 54/0.2

x < 270

Тоб-то x∈(−∞; 270)

Тому треба обрати пункт "Г".

Графік функції, визначеної на проміжку [−5; 4], проходить через одну з наведених точок (див. рисунок). Укажіть цю точку.

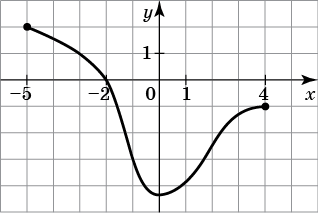
Оберіть вірну відповідь:

А (−5; -2)

Б (1; -2)

В (−1; 4)

Г (−3; 1)

Д (0; -2)

Перевірка показує, що точка з координатами (–3; 1) належить даному графіку.

Тому треба обрати пункт "Г".

Сергій і Петро збирали яблука. Сергій зібрав яблук у 5 разів більше, ніж Петро. Яку частину усіх яблук зібрав Петро?

Оберіть вірну відповідь:

А 15

Б 16

В 12

Г 56

Д 45

Нехай Петро зібрав x кілограмів яблук (це одна частина).

Тоді Сергій зібрав 5x кілограмів яблук (це 5 частин).

Всього яблук: x + 5x = 6x кілограмів (це 6 частин).

Тому Петро зібрав x6x = 16 частину усіх яблук.

Тому треба обрати пункт "Б".

На рисунку зображено куб ABCDA₁B₁C₁D₁. Яка з наведених прямих паралельна площині (AA₁B₁)?

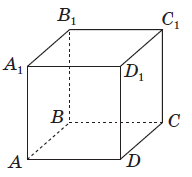
Оберіть вірну відповідь:

А BC

Б BD

В C₁D

Г CB₁

Д A₁B

Пряма C₁D паралельна прямій B₁A.

Пряма B₁A лежить в площині AA₁B₁.

Тому прямая C₁D паралельна площині AA₁B₁ за ознакою паралельності прямої та площини.

Тому треба обрати пункт "В".

Розв'яжіть рівняння 4^x = 8.

Оберіть вірну відповідь:

А 12

Б 23

В 32

Г 26

Д 325

4^x = 8

2^2x = 2³

2x = 3

x = 32

Тому треба обрати пункт "В".

На рисунку зображено прямокутний трикутник з катетами a и b, гіпотенузою c і гострим кутом α. Укажіть правильну рівність.

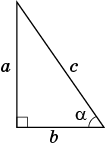
Оберіть вірну відповідь:

А cos α = ab

Б cos α = cb

В cos α = ac

Г cos α = ca

Д cos α = bc

В даному трикутнику c — гіпотенуза, b — катет, прилеглий до кута α.

Косинус кута — відношеня прилеглого катета до гіпотенузи.

Тому cos α = bc

Тому треба обрати пункт "Д".

Випущено партію з 300 лотерейних білетів. Імовірність того, що навмання вибраний білет із цієї партії буде виграшним, орівнює 0,2. Визначте кількість білетів без виграшу серед цих 300 білетів.

Оберіть вірну відповідь:

А 6

Б 60

В 294

Г 150

Д 240

Ймовірність того, що навмання обраний білет буде виграшним — відношеня кількості виграшних білетів до кількості всіх білетів.

0,2 = Кількість виграшних квитків300

Кількість виграшних квитків = 0,2 · 300 = 60

Тому кількість квитків без виграшу дорівнює 300 - 60 = 240

Тому треба обрати пункт "Д".

Спростіть вираз 11 + tg²α.

Оберіть вірну відповідь:

А cos²α

Б sin²α

В tg²α

Г ctg²α

Д 1

1	=	1	= cos²α
1 + tg²α	=	1	= cos²α
		cos²α

Тому треба обрати пункт "А".

На якому рисунку зображено ескіз графіка функції y = √x − 2?

Оберіть вірну відповідь:

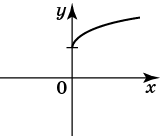
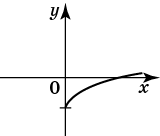
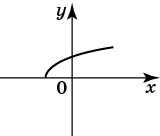
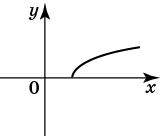
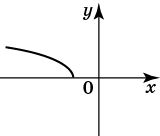
Нескладно намалювати графік y = √x

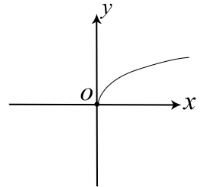
Щоб з нього отримати графік функції y = √x − 2, необхідно його змістити вправо вздовж осі Ox на 2 одиниці:

Тому треба обрати пункт "Г".

На діагоналі AC квадрата ABCD задано точку, відстань від якої до сторін AB і BC дорівнює 2 см і 6 см відповідно. Визначне периметр квадрата ABCD.

Оберіть вірну відповідь:

А 16 см

Б 24 см

В 32 см

Г 48 см

Д 64 см

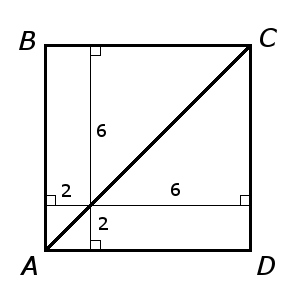
Відстань від точки до прямої — це довжина перпендикуляра, опущеного з точки на пряму.

Тому AB = 2 + 6 = 8

P_ABCD = 4AB = 4·8 = 32(см)

Тому треба обрати пункт "В".

Розв'яжіть систему рівнянь 3√x = 12, x - 2y = 26.

Для одержаного розв'язку (x₀; y₀) системи обчисліть суму x₀ + y₀.

Оберіть вірну відповідь:

А 11

Б 21

В -7

Г -10

Д -14

3√x = 12 x - 2y = 26

√x = 12/3 = 4 x - 2y = 26

x = 4² = 16 x - 2y = 26

x = 16 16 - 2y = 26

x = 16 - 2y = 26 - 16 = 10

x = 16 y = 10/(-2) = -5

x₀ + y₀ = 16 + (-5) = 16 - 5 = 11

Тому треба обрати пункт "A".

Висота правильної чотирикутної піраміди дорівнює 3 см, а сторона її основи — 12 см. Знайдіть довжину бічного ребра піраміди.

Оберіть вірну відповідь:

А 6 см

Б 3√5 см

В 5√3 см

Г 9 см

Д 15 см

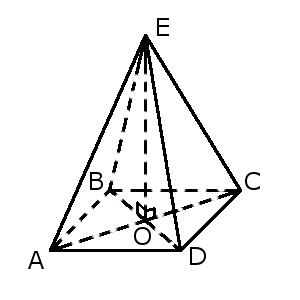
Основа правильної чотирикутної піраміди — квадрат.

Якщо сторона квадрату — 12 см, то його діагональ:

AC² = AB² + BC² = 12² + 12² = 288

AC = √288 = 12√2 (см)

Діагоналі квадрату точкою перетину діляться навпіл, тому

OC = AC/2 = 6√2 (см)

З трикутника ΔOEC (∠O=90°) за теоремою Піфагора

EC² = OE² + OC² = 3² + (6√2)² = 9 + 72 = 81

EC = √81 = 9 (см)

Тому треба обрати пункт "Г".

Яку властивість із наведених має функція y = 2x − 9?

Оберіть вірну відповідь:

А є парною

Б є непарною

В є періодичною

Г є спадною

Д є зростаючою

Функція парна, якщо виконується тотожність f(x) = f(-x)
В нашому випадку y(-x) = 2(-x) − 9 = -2x − 9 ≠ y(x)
це означає, що функція не є парною;
Функція непарна, якщо виконується тотожність f(-x) = -f(x)
В нашому випадку y(-x) = 2(-x) − 9 = -(2x + 9) ≠ -y(x)
це означає, що функція не є непарною;
Функція періодічна, якщо існує ненульове значення T, таке що f(x + T) = f(x)
В нашому випадку y(x + T) = 2(x + T) − 9 = 2x + 2T + 9
Щоб знайти період прирівняємо y(x + T) та y(x)
2x + 2T + 9 = 2x + 9
2T = 0
T = 0
це означає, що функція не є періодичною;
Щоб дізнатися спадна чи зростаюча функція достатньо взяти похідну
y ' = 2
так як похідна для будь-якого x буде додатньою >0, то функція є зростаючою.

Тому треба обрати пункт "Д".

Розв'язати рівняння |x|10 = 2.

Оберіть вірну відповідь:

А -5; 5

Б -20; 20

В 20

Г 5

Д -0,2; 0,2

|x|10 = 2

|x| = 2·10 = 20

x = ±20

Тому треба обрати пункт "Б".

Лист заліза, що має форму прямокутника ABCD (AB = 50 см), згортають таким чином, щоб отримати циліндричну трубу (див. рисунки 1 і 2). Краї AB і CD зварюють між собою без накладання одного краю на інший. Обчисчліть площу бічної поверхні отриманого циліндра (труби), якщо діаметр його основи дорівнює 20 см.

Оберіть відповідь, найближчу до точної. Товщиною листа заліза та швом від зварюваня знехтуйте.

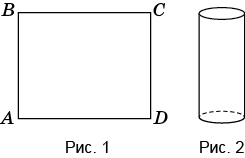
Оберіть вірну відповідь:

А 1570 см²

Б 3150 см²

В 5240 см²

Г 6300 см²

Д 1000 см²

Площа бокової поверхні даного циліндра — це площа прямокутника ABCD.

Довжина окружності основи циліндра:

πd = 20π (см) — це довжина сторони AD прямокутника ABCD.

Тоді S_ABCD = AB·AD = 50·20π = 1000π ≈ 3140 (см²).

Тому треба обрати пункт "Б".

Укажіть проміжок, якому належить число log₅4.

Оберіть вірну відповідь:

А (0; 1)

Б (1; 2)

В (2; 3)

Г (3; 4)

Д (4; 5)

log₅x - зростаюча функція, це означає що:

log₅1 < log₅4 < log₅5

0 < log₅4 < 1

Тому треба обрати пункт "A".

Укажіть рівняння прямої, яка може бути дотичною до графіка функції y = f(x) у точці з абсцисою x₀ = 2, якщо f '(2) = −3.

Оберіть вірну відповідь:

А y = -32x + 1

Б y = 3x - 2

В y = 2x + 3

Г y = 32x - 1

Д y = -3x + 2

f '(x₀) — кутовий коефіціент в рівнянні дотичної, проведеної до графіку функції y = f(x) в точці x₀.

За умовою: f '(x₀) = f '(2) = −3.

Тому рівняння дотичної до функції f(x) у точці x₀ = 2 буде мати вигляд: y = f '(2)x + b= -3x + b

Так як коефіцієнт зсуву b невідомий, то вибираємо правильну відповідь по кутовому коефіцієнту f '(2) = −3.

Тому треба обрати пункт "Д".

Розв'яжіть нерівність (x - 6)(x + 2)²x - 3 ≤ 0.

Оберіть вірну відповідь:

А {−2}∪(3; 6]

Б (−∞; −2]∪(3; 6]

В [−2; 6]

Г (−∞; 6]

Д (−∞; 3)∪(3; 6]

(x - 6)(x + 2)²x - 3 ≤ 0

Застосуємо метод інтервалів

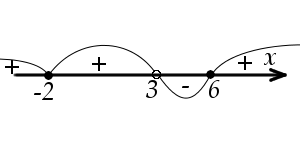
Тому, x∈{−2}∪(3;6].

Тому треба обрати пункт "А".

Установіть відповідність між функцією (1—4) та координатними чвертями (А—Д), у яких розміщений графік цієї функції (координатні чверті показано на рисунку).
зно 2015 1 завдання 21

Функція	Координатні чверті
1 y = - x² - 1 2 y = x + 1 3 y = - 1x 4 y = cos x	A II і IV Б III і IV В І, II і III Г І, III і IV Д І, II, III і IV

Оберіть вірні відповіді:

	А	Б	В	Г	Д
1
2
3
4

Намалюємо ескізи графіков заданих функцій:

y = - x² - 1

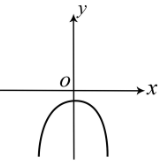
Цей графік лежить в III і IV чвертях

Тому треба обрати пункт "Б".
y = x + 1

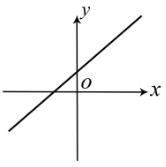
Цей графік лежить в І, II і III чвертях

Тому треба обрати пункт "В".
y = - 1x

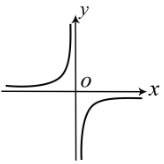
Цей графік лежить в II і IV чвертях

Тому треба обрати пункт "А".
y = cos x

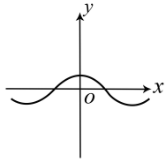
Цей графік лежить в І, II, III і IV чвертях

Тому треба обрати пункт "Д".

Установіть відповідність між твердженням про дріб (1—4) та дробом (А—Д), для якого це твердження є правильним.

Твердження про дріб	Дріб
1 є оберненим до дробу 125 2 менший за 0,5 3 є неправильним 4 є скоротним	A 57 Б 1327 В 4110 Г 710 Д 3451

Оберіть вірні відповіді:

	А	Б	В	Г	Д
1
2
3
4

125 = 75 - є оберненим до дробу 57
Тому треба обрати пункт "А".
1327 = 2654 < 2754 = 12
Тому треба обрати пункт "Б".
неправильним є дріб, у якого чисельник більше або дорівнює знаменнику;
4110 - неправильний дріб

Тому треба обрати пункт "В".
3451 = 23 - дріб є скоротним
Тому треба обрати пункт "Д".

Установіть відповідність між геометричною фігурою (1—4) та її площею (А—Д).
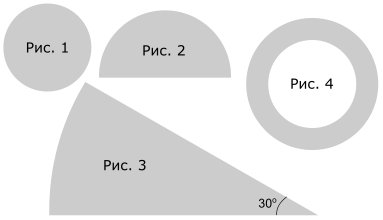
зно 2015 1 завдання 23

Геометрична фігура	Площа геометричної фігури
1 круг радіуса 4 см (рис. 1) 2 півкруг радіуса 6 см (рис. 2) 3 сектор радіуса 12 см з градусною мірою центрального кута 30° (рис. 3) 4 кільце, обмежене колами радіусів 4 см і 6 см (рис. 4)	A 12π см² Б 16π см² В 18π см² Г 20π см² Д 24π см²

Оберіть вірні відповіді:

	А	Б	В	Г	Д
1
2
3
4

S_круга = πr² = 16π (см²)
Тому треба обрати пункт "Б".
S_{полукруга} = πr²2 = 36π2 = 18π (см²)
Тому треба обрати пункт "В".
Sсектора = πr²n°360° = 144π · 30°360° = 12π (см²)
Тому треба обрати пункт "А".
S_кольца = 36π − 16π = 20π (см²)
Тому треба обрати пункт "Г".

У прямокутній декартовій системі координат у просторі xyz задано точки A (2;0;0) і B (-4;2;6). До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, щоб утворилося правильне твердження.

Початок речення	Закінчення речення
1 Проекцією точки B на вісь y є точка 2 Проекцією точки B на площину xz є точка 3 Вектор AB має координати 4 Серединою відрізка AB є точка	A (−1; 1; 3). Б (0; 2; 0). В (−4; 0; 6). Г (−6; 2; 6). Д (−2; 2; 6).

Оберіть вірні відповіді:

	А	Б	В	Г	Д
1
2
3
4

Точка на осі Oy має координати (0; y; 0), тому проекцією точки B на вісь Oy є точка з координатами(0; 2; 0).
Тому треба обрати пункт "Б".
Точка на площині XZ має координат (x; 0; z), тому проекцією точки B на площину XZ є точка з координатами (−4; 0; 6).
Тому треба обрати пункт "В".
Координаты вектора AB = (B_x - A_x; B_y - A_y; B_z - A_z) = (-4 - 2; 2 - 0; 6 - 0) = (-6; 2; 6)
Тому треба обрати пункт "Г".
Серединою відрізка AB є точка C з координатами
C_x = A_x + B_x2 = 2 - 42 = -1
C_y = A_y + B_y2 = 0 + 22 = 1
C_z = A_z + B_z2 = 0 + 62 = 3
Тобто, C(-1, 1, 3)
Тому треба обрати пункт "А".

У магазині в продажу є лише музичні диски, диски з науково-популярними фільмами та диски з художніми фільмами. Кількість дисків із науково-популярними фільмами в п'ять разів більша за кількість музичних дисків і вдвічі менша за кількість дисків із художніми фільмами. Загальна кількість дисків у цьому магазині дорівнює 192.

1 Скільки відсотків становить кількість музичних дисків від загальної кількості всіх дисків у магазині?

2 Визначте кількість дисків із науково-популярними фільмами в цьому магазині.

Впишіть відповіді:

Позначимо кількість музикальних дисків x. Тоді кількість науково-популярних дисків — 5x, а кількісті художніх дисків — 10x. Загальна кіллькість дисків дорівнює x + 5x + 10x = 16x, а за умовою це 192 диска. Тобто,
16x = 192

x = 192/16 = 12.

Значить, усього музикальних дисків — 12. Процент, який вони складають від загальної кількості дисків:

12192·100% = 116·100% = 25%4 = 6,25%.
Позначимо кількість музикальних дисків x. Тоді кількість науково-популярних дисків — 5x, а кількісті художніх дисків — 10x. Загальна кіллькість дисків дорівнює x + 5x + 10x = 16x, а за умовою це 192 диска. Тобто,
16x = 192

x = 192/16 = 12.

Значить+, усього музикальних дисків — 12. Визначимо кількість науково-популярних дисків:

5x = 5·12 = 60.

3 вершини тупого кута B паралелограма ABCD опущено перпендикуляр BO на сторону AD. Коло з центром у точці A проходить через вершину B та перетинає сторону AD в точці K. Відомо, що AK=6 см, KD=4 см, AO=5 см.

1 Визначте периметр паралелограма ABCD (у см).

2 Обчисліть довжину діагоналі BD (у см).

Впишіть відповіді:

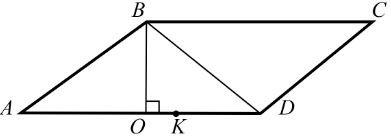
AB = AK як радіуси кола з центром в точці A.
AB = AK = 6 см;

AD = AK + KD = 6 + 4 = 10 см;

P_ABCD = 2(AB + AD) = 2(6 + 10) = 2·16 = 32 (см).
OK = AK − AO = 6 — 5 = 1 (см).
OD = OK + KD = 1 + 4 = 5 (см).

В трикутнику ABD висота BO є медіаною (AO = OD = 5 см), це означає, що трикутник ABD — рівнобічний. AB = BD = 6 см.

Плавець під час першого тренування подолав дистанцію у 450 м. Кожного наступного тренування він пропливав на 50 м більше, ніж попереднього, поки не досягнув результату 1000 м за одне тренування. Після цього під час кожного відвідування басейну плавець пропливав 1000 м. Скільки всього кілометрів плавець проплив за перші 10 тижнів тренувань, якщо він тренувався тричі кожного тижня?

Впишіть відповідь:

1. Кількість тренувань, яку провів спортсмен, поки досягнув результату 1000 м.

1000 − 45050 + 1 = 12.

Порахуємо відстань, яку проплив спортсмен за перші 12 тренувань. Для цього розглянемо арифметичну прогресію, членами якої є результати перших 12 тренувань. Тоді:

a₁ = 450 м;

a₁₂ = 1000 м.

Знайдемо суму всіх членів цієї прогресії — це і буде шукана відстань:

S₁₂ = a₁ + a₁₂2·12 = 450 + 10002·12 = 725·12 = 8700 (м)=8,7 (км).

3. 12 тренувань — це 4 тижні.

За останні 6 тижнів спортсмен провів 6·3 = 18 тренувань, тобто, проплив

18·1000 = 18000 (м) = 18 (км).

4. Всього за 10 тижнів спортсмен проплив 8,7 + 18 = 26,7 кілометрів.

Розв'яжіть рівняння log₅²x + log₅x = 2. Якщо рівняння має один корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то у відповіді запишіть їхню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100.

Впишіть відповідь:

ОДЗ рівняння: x > 0.

Нехай log₅x = a.

Тоді отримаємо рівняння a² + a − 2 = 0,

коренями якого є числа a₁ = –2; a₂ = 1. Значить,

log₅x = -2 log₅x = 1 => x = 125 x = 5

Сума коренів рівняння:

125 + 5 = 0,04 + 5 = 5,04

Обчисліть значення виразу 10a + bb² - 4a² + 4a + 2bb² + 4ab + 4a² при a = 0,25, b = 4,5.

Впишіть відповідь:

10a + bb² - 4a² + 4a + 2bb² + 4ab + 4a² = 10a + bb² - 4a² + 2(2a + b)(b + 2a)² = 10a + b(b - 2a)(b + 2a) + 2(b + 2a) = 10a + b + 2(b - 2a)(b - 2a)(b + 2a) = 10a + b + 2b - 4a(b - 2a)(b + 2a) = 6a + 3b(b - 2a)(b + 2a) = 3(2a + b)(b - 2a)(b + 2a) = 3b - 2a

Якщо a = 0,25; b = 4,5, то:

3b - 2a = 34,5 - 2·0,25 = 34,5 - 0,5 = 34 = 0,75.

Навколо конуса описано трикутну піраміду, площа основи якої дорівнює 50√3, а периметр основи — 50. Визначте об'єм V цього конуса, якщо довжина його твірної дорівнює 4. У відповіді запишіть значення Vπ.

Впишіть відповідь:

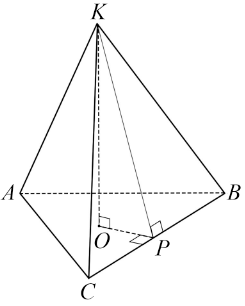
На рисунку
KO — висота піраміди і вписаного в неї конуса;
OP — радіус кола, вписаного в основу піраміди, тобто радіус основи конуса;
KP — твірна конуса.

Площа основи піраміди обчислюється за формулою площі трикутника S = pr, де p — півпериметр трикутника, r — радіус вписаного в цей трикутник кола.

Тоді r = Sp = 50√325 = 2√3 = OP.

З прямокутного трикутника KOP (∠O=90°) за теоремою Піфагора маємо:

KO² = KP² − OP² = 4² - (2√3)² = 16 - 12 = 4

KO = √4 = 2

Об'єм конуса:

V_конуса = 13 S_{основи конуса}·KO = 13πr²·KO =13π·(2√3)²·2 = 8π

Vπ = 8ππ = 8.

Ви не виконали всі завдання!
Ви впевнені, що бажаєте завершити тестування?

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!