Онлайн тест ЗНО з математики 2016 року (варіант 2)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

Витрачено часу: 0

Вправа 1 з 33

Витрачено часу: 0

Вправа 1 з 33

На рисунку зображено прямі m і n, що перетинаються визначте градусну міру кута γ, якщо α + β = 50°.

Оберіть вірну відповідь:

А 310°

Б 155°

В 145°

Г 140°

Д 130°

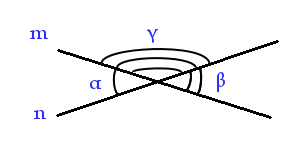
Кути α та β - вертикальні кути, це означає що α = β

2α = 50° => α = 25°

Кути α та γ - суміжні кути, це означає що α + γ = 180°

γ = 180° - α = 180° - 25° = 155°

Тому треба обрати пункт "Б".

Відео

Укажіть число, що є розв'язком нерівності 5x - 3 ≥ 1

Оберіть вірну відповідь:

А -2

Б 0

В 2

Г 4

Д 9

5x - 3 -1 ≥ 0

5 - x + 3x - 3 ≥ 0

8 - xx - 3 ≥ 0

x - 8x - 3 ≤ 0

застосуємо метод інтервалів

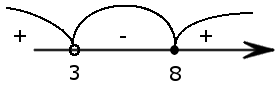
x є (3; 8]

Тому треба обрати пункт "Г".

Відео

0,4 x² · 5 x³ =

Оберіть вірну відповідь:

А 2 x⁶

Б 20 x⁵

В 2 x⁵

Г 0,2 x⁵

Д 0,2 x⁶

0,4 x² · 5 x³ = 0,4 · 5 x^{3 + 2} = 2 x⁵

Тому треба обрати пункт "B".

Відео

Розв'яжіть систему рівнянь x + y = 5, 4^x = 16^-1

Якщо (x₀; y₀) - розв'язок цієї системи, то x₀·y₀ =

Оберіть вірну відповідь:

А -36

Б -14

В -6

Г 4

Д 6

Розв'яжемо систему рівнянь x + y = 5, 4^x = 16^-1

З другого рівняння

4^x = 16^-1 = (4²)^-1 = 4^-2

x = -2

Підставимо x в перше рівняння

-2 + y = 5

y = 5 + 2 = 7

Отже x₀·y₀ = (-2) · 7 = -14

Тому треба обрати пункт "Б".

Відео

Графіком однієї з наведених функцій є пряма. Укажіть цю функцію:

Оберіть вірну відповідь:

А y = 2^x

Б y = x² - 2x

В y = cos (2x)

Г y = 2x

Д y = 2x

Рівняння прямої має вигляд y = kx + b

де k і b певні числа

Такий вигляд має лише одне з рівнянь, а саме y = 2x.

Тому треба обрати пункт "Г".

Відео

Якому значенню серед наведених може дорівнювати довжина сторони AC трикутника ABC, якщо AB = 3 см, BC = 10 см?

Оберіть вірну відповідь:

А 3 см

Б 5 см

В 7 см

Г 11 см

Д 15 см

Всім трикутникам притаманна властивість: "Сума довжин двох сторін трикутника завжди більша за довжину третьої його сторони."

скориставшись цією властивістю запишемо нерівності які дозволять оцінити довжину сторони AC.

AB + BC > AC => 3 + 10 > AC => AC < 13

AB + AC > BC => 3 + AC > 10 => AC > 10 - 3 => AC > 7

BC + AC > AB => 10 + AC > 3 => AC > 3 - 10 => AC > -7

Цим умовам задовільняє довжина 11 см

Тому треба обрати пункт "Г".

Відео

Спростіть вираз ab(a - b) - ba(a - b).

Оберіть вірну відповідь:

А a + bab

Б 1ab

В 1b - a

Г a - bab

Д 0

ab(a - b) - ba(a - b) = a²ab(a - b) - b²ab(a - b) =

= a² - b²ab(a - b) = (a - b)(a + b)ab(a - b) = a + bab

Тому треба обрати пункт "A".

Відео

У прямокутній системі координат у просторі на осі z вибрано точку M (див. рисунок). Серед наведених варіантів укажіть можливі координати цієї точки.

Оберіть вірну відповідь:

А (1; 0; 0)

Б (1; 1; 0)

В (0; 0; 1)

Г (0; 0; -1)

Д (0; 1; 0)

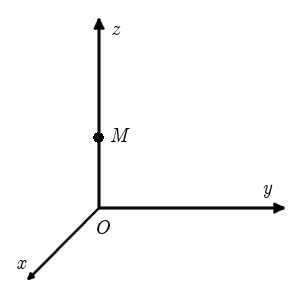
Так як точка M(M_x; M_y; M_z) лежить на додатному напрямку осі z, то координати M_x = 0, M_y = 0, M_z > 0.

Тому треба обрати пункт "В".

Відео

Задано арифметичну прогресію (a_n) у якій різниця d = 0,5, п'ятнадцятий член a₁₅ = 12. Визначте перший член прогресії a₁.

Оберіть вірну відповідь:

А 24

Б 12,5

В 6

Г 5

Д 4,5

Скористаємось формулою n-того члена арифметичної прогресії

a_n = a₁ + (n - 1)d

12 = a₁ + (15 - 1)0,5

a₁ = 12 - 14 · 0,5 = 12 - 7 = 5

Тому треба обрати пункт "Г".

Відео

На рисунку жирними точками позначено річні мінімуми площі поверхні арктичного льоду, що спостерігалися в період з 2004 р. по 2014 р. (для наочності точки з'єднані відрізками). По горизонталі відмічено роки, а по вертикалі - площу поверхні льоду (у млн км²). Користуючись наведеною інформацією, визначте із заданого періоду рік, у якому величина річного мінімуму площі поверхні льоду змінилась найбільше порівняно з попереднім роком.

Оберіть вірну відповідь:

А 2006 р.

Б 2007 р.

В 2009 р.

Г 2012 р.

Д 2013 р.

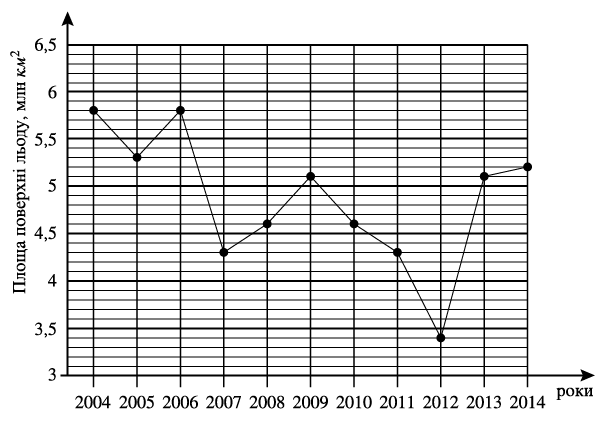
З графіку визначимо різницю з попередніми роками для запропонованих варіантів відповідей

2005 - 2006: 0,5

2006 - 2007: 1,5

2008 - 2009: 0,5

2011 - 2012: 0,9

2012 - 2013: 1,7

Можна бачити що максимальна різниця припадає на 2012 - 2013

Тому треба обрати пункт "Д".

Відео

Прямі a та b мимобіжні. Які з наведених тверджень є правильними

Прямі a та b перетинаються
Прямі a та b лежать в одній площині
Існує пряма паралельна прямій a, що перетинає пряму b

Оберіть вірну відповідь:

А Лише I

Б Лише II

В Лише I та II

Г Лише III

Д I, II та III

Дві прямі називаються мимобіжними, якщо вони не належать одній площині

Так як прямі не належать одній площині, то вони не перетинаються

Пункт III - є однією з властивостей мимобіжних прямих

Тому треба обрати пункт "Г".

Відео

Якому проміжку належить число ³√18

Оберіть вірну відповідь:

А [0; 1)

Б [1; 2)

В [2; 3)

Г [3; 4)

Д [4; +∞)

³√8 < ³√18 < ³√27

³√2³ < ³√18 < ³√3³

2 < ³√18 < 3

Тому треба обрати пункт "В".

Відео

log₂ 5 + log₂ 1,6 =

Оберіть вірну відповідь:

А 3

Б 3,3

В 0,25

Г 4

Д log₂ 6,6

Скористаємось властивістю суми логарифмів

log₂ 5 + log₂ 1,6 = log₂ (5 · 1,6) = log₂ 8 = log ₂ 2³ = 3

Тому треба обрати пункт "A".

Екрани телевізорів, зображених на рис. 1 і 2, мають форму прямокутників, відповідні сторони яких пропорційні. Діагоналі екранів цих телевізорів дорівнюють відповідно 32 дюйми і 48 дюймів. Визначте у скільки разів площа екрана зображеного на рис. 2, більша за площу телевізору зображеного на рис. 1.

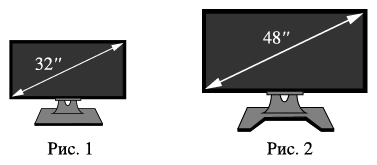
Оберіть вірну відповідь:

А в 1,5 рази

Б у 16 разів

В у 2,56 раза

Г у 4 раза

Д у 2,25 раза

Запишемо формулу площі прямокутника через довжини діагоналей

S=12d² sin α де d - довжина діагоналі
α - кут між діагоналями

Тоді площа екрана першого телевізора:

S₁ = 12d₁² sin α = 1232² sin α = 512 sin α

площа екрана другого телевізора:

S₂ = 12d₂² sin α = 1248² sin α = 1152 sin α

Відношення площі другого телевізора до площі першого

S₂S₁ = 1152 sin α512 sin α = 2,25

Тому треба обрати пункт "Д".

Відео

Обчисліть значення виразу 4sin² α, якщо 4cos² α = 1;

Оберіть вірну відповідь:

А 3

Б 34

В 14

Г 4

Д 0

Скористаємося формулою sin² α + cos² α = 1

4(sin² α + cos² α) = 4

4sin² α = 4 - 4cos² α = 4 - 1 = 3

Тому треба обрати пункт "А".

Відео

Використовуючи формулу Ньютона-Лейбніца, обчисліть ∫ 1 2 6x²dx

Оберіть вірну відповідь:

А 12

Б 14

В 18

Г 22

Д 42

∫ 1 2 6x²dx = (2x³) | 1 2 = 2·2³ - 2·1³ = 2·8 - 2·1 = 16 - 2 = 14

Тому треба обрати пункт "Б".

Відео

Визначте об'єм правильної трикутної призми, бічні грані якої є квадратами, а периметр основи дорівнює 12.

Оберіть вірну відповідь:

А 16√3

Б 64

В 48

Г 64√3

Д 576

Намалюємо правильну трикутну призму

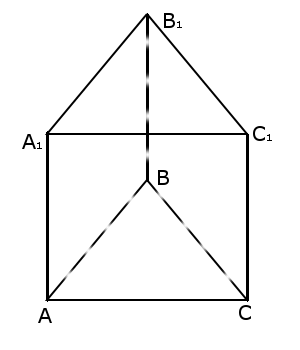
Бічними гранями нашої призми є квадрати. У квадратів сторони рівні це означає

З квадрату AA₁B₁B => AA₁ = AB = BB₁ = A₁B₁

З квадрату AA₁C₁C => AA₁ = AC = CC₁ = A₁C₁

З квадрату BB₁C₁C => BB₁ = BC = CC₁ = B₁C₁

тобто

AA₁ = BB₁ = CC₁ = AB = BC = AC = A₁B₁ = B₁C₁ = A₁C₁

Так як AB = BC = AC, то трикутник ABC правильний. Тому знаючи довжину периметру трикутника ABC, можемо знайти довжини сторін трикутника

P = AB + BC + AC = 3AB

AB = P/3 = 12/3 = 4

відповідно AA₁ = BB₁ = CC₁ = AB = BC = AC = A₁B₁ = B₁C₁ = A₁C₁ = 4

Об'єм правильної призми можна визначити за формулою

V = S_ос · h
де S_ос - площа основи призми
h - висота призми.

Так як призма правильна, то h = AA₁ = 4

Площу правильного трикутника ABC визначити за формулою:

S_ABC = √34 AB² = √34 4² = 4√3

тепер можемо знайти об'єм призми

V = S_ос · h = S_ABC · AA₁ = 4√3 · 4 = 16√3

Тому треба обрати пункт "А".

Відео

Яка з наведених парабол може бути графіком функції y = x² + px + q, якщо рівняння x² + px + q = 0 не має дійсних коренів?

Оберіть вірну відповідь:

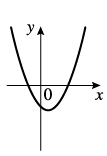
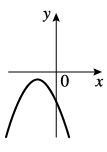
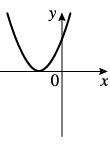
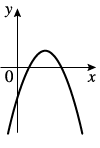
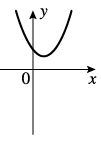
y = ax² + px + q - це парабола.

Якщо a > 0, то вітки у параболи вгору, якщо a < 0, то вітки у параболи вниз

В нашому випадку a = 1, це означає що вітки параболи будуть вгору. Тому відповіді "Б" і "Г" не підходять, бо на наведених графіках вітки у парабол ідуть вниз.

x² + px + q = 0 не має дійсних коенів

- це означає що графік не перетинає і не торкається вісі Ox

Графік "А" перетинає вісь Ox - це означає, що рівняння x² + px + q = 0 має два дійсних кореня

Графік "В" дотикається до вісі Ox - це означає, що рівняння x² + px + q = 0 має один дійсний корінь

Тому треба обрати пункт "Д".

Відео

Розв'яжіть рівняння 3· sin xcos x = √3

Оберіть вірну відповідь:

А π6 + πn, n ∈ Z

Б π3 + πn, n ∈ Z

В π6 + 2πn, n ∈ Z

Г ±π6 + 2πn, n ∈ Z

Д π9 + πn3 , n ∈ Z

Розвя'жемо тригонометричне рівняння

3· sin xcos x = √3

tg x = √33

x = π6 + πn, n ∈ Z

Тому треба обрати пункт "А".

Відео

Розв'яжіть нерівність log₃ x < -1

Оберіть вірну відповідь:

А (13; +∞)

Б (-∞; 13)

В (-13; 0)

Г (0; 13)

Д (-∞; -3)

log₃ x < -1

ОДЗ: x > 0

так як основа логарифма більша одиниці, то

3^{log₃ x} < 3^-1

x < 13

З урахуванням ОДЗ x ∈ (0; 13)

Тому треба обрати пункт "Г".

Відео

На рисунках (1-5) зображено графіки функцій, визначених на відрізку [-3; 3]
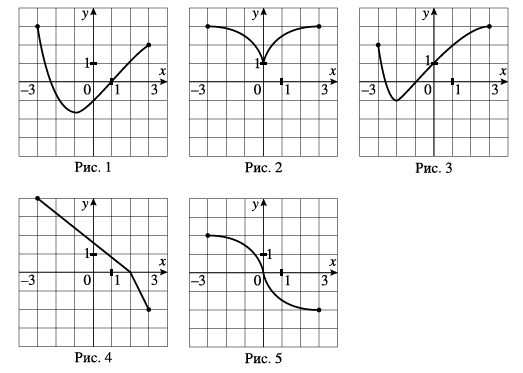
зно 2016 2 завдання 21

До кожного запитання (1-4) оберіть вірну відповідь (А-Д)

Запитання

Відповідь

1	На якому рисунку зображено графік функції, що проходить через точку (1; 0)?
2	На якому рисунку зображено графік парної функції?
3	На якому рисунку зображено графік функції, що має дві спільні точки з графіком функції y = log_1/3 x
4	На якому рисунку зображено графік функції, що зростає на відрізку [-2; 3]

A рис. 1

Б рис. 2

В рис. 3

Г рис. 4

Д рис. 5

Оберіть вірні відповіді:

	А	Б	В	Г	Д
1
2
3
4

Знайдемо рисунок, на якому зображено графік функції, що проходить через точку (1; 0). Бачимо, що серед усіх графіків лише графік на рис. 1 проходить через точку (1; 0). Отже першому запитанню відповідає пункт "A".
Парна функція, це функція симетрична відносно осі Ox. Отже другому запитанню відповідає рисунок 2 - пункт "Б".
Функція y = log_1/3 x - спадна ОДЗ x > 0
log_1/3 1/9 = 2
log_1/3 1/3 = 1
log_1/3 1 = 0
log_1/3 3 = -1
відповідно, ця функція перетинає в двох точках лише функцію зображену на рисунку 4 - пункт "Г".
На відрізку [-2; 3] зростає функція зображена на рисунку 3 - пункт "В".

Відео

Установіть відповідність між числовим виразом (1—4) та його значенням (А—Д), якщо a = 254.

Вираз	Значеня виразу
1 2a3 2 1a 3 \|9 - 2a\| 4 a^1/2	A 425 Б 212 В -312 Г 312 Д 416

Оберіть вірні відповіді:

	А	Б	В	Г	Д
1
2
3
4

2a3 = 23·254 = 256 = 416
Тому треба обрати пункт "Д".
1a = 1 : 254 = 1 · 425 = 425
Тому треба обрати пункт "А".
|9 - 2a| = |9 - 2·254| = |9 - 252| = |9·2 - 252| = |18 - 252| = |-72| = 72 = 312
Тому треба обрати пункт "Г".
a^1/2 = (254)^1/2 = 52 = 212
Тому треба обрати пункт "Б".

Відео

На рисунку зображено коло з центром в точці О, радіус якого дорівнює 6. Хорду BC видно з центру кола під кутом 60°, BK - діаметр. Через точку A до кола проведено дотичну AB, причому OA = 2AB. Установіть відповідність між відрізком (1-4) та його довжиною (А-Д)
зно 2016 2 завдання 23

Відрізок	Довжина відрізку
1 BK 2 AB 3 BC 4 CK	A 6 Б 2√3 В 12 Г 6√3 Д 3√3

Оберіть вірні відповіді:

	А	Б	В	Г	Д
1
2
3
4

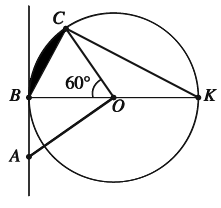
BK - діаметр. BK = r = 2·6 = 12
Тому треба обрати пункт "В".
Трикутник AOB прямокутний. AO - гіпотенуза. Так-як AO = 2AB то кут AOB = 30°
AB = BO ·tg ∠AOB = BO ·tg 30° = 6·√33 = 2√3
Тому треба обрати пункт "Б".
Трикутник СOB рівнобедрений OB = OC = r
∠BCO = ∠CBO = (180°-60°)/2 = 60°
Так як всі кути рівні то трикутник СOB - рівносторонній. BC = OB = OC = r = 6
Тому треба обрати пункт "А".
Трикутник BCK - прямокутний, так-як спирається на діаметр. ∠CBO = 60°
CK = BK sin 60° = 12·√32 = 6√3
Тому треба обрати пункт "Г".

Відео

Установіть відповідність між геометричним тілом (1-4) та площею його повної поверхні (А-Д).

Геометричне тіло	Площа повної поверхні
1 циліндр з радіусом основи 3 та висотою 4 2 конус з радіусом основи 3 та твірною 5 3 куб з ребром √3π 4 куля радіуса 2√3	A 18π Б 24π В 36π Г 42π Д 48π

Оберіть вірні відповіді:

	А	Б	В	Г	Д
1
2
3
4

S = 2S_ос + S_б = 2·(πr²) + 2πrh = 2π·3² + 2π·3·4 = 18π + 24π = 42π
Тому треба обрати пункт "Г".
S = S_ос + S_б = πr² + πrl = π·3² + π·3·5 = 9π + 15π = 24π
Тому треба обрати пункт "Б".
S = 6a² = 6·(√3π)² = 6·3π = 18π
Тому треба обрати пункт "А".
S = 4πr² = 4π(2√3)² = 4π·12 = 48π
Тому треба обрати пункт "Д".

Відео

У бібліотеці є лише підручники, словники та книги з художньої літератури. Відсотковий розподіл кількості цих книг у бібліотеці відображено на діаграмі.

1 Визначте загальну кількість книг у цій бібліотеці, якщо кількість підручників дорівнює 84.

2 Скільки потрібно придбати додатково підручників, щоб отримана після цього їхня сумарна кількість відносилася до кількості довідників як 4:1?

Впишіть відповіді:

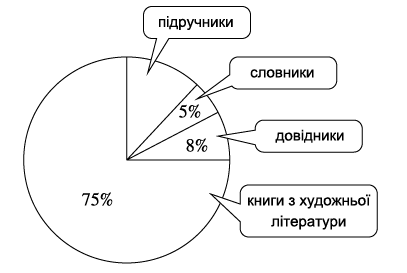
Знайдемо відсоткову частку підручників в бібліотеці
відсоткова частка підручників = 100% - 75% - 8% - 5% = 12%

Складемо пропорцію для визначення загальної кількості книжок в бібліотеці

загальна кількості книжок - 100%

кількість підручників - 12%

тоб-то
загальна кількості книжоккількість підручників = 100%12%

загальна кількості книжок = кількість підручників · 100%12% = 84 · 100%12% = 700
Знайдемо кількість довідників в бібліотеці
Складемо пропорцію для визначення кількості довідників в бібліотеці

кількісті довідників - 8%

загальна кількості книжок - 100%

тоб-то
кількісті довідниківзагальна кількості книжок = 8%100%

кількісті довідників = загальна кількості книжок · 8%100% = 700 · 8%100% = 56

підручників має стати в 4 рази більше ніж довідників

підручників має стати: 4· 56 = 224

необхідно докупити: 224 - 84 = 140 (підручників)

Відео

На рисунку зображено квадрат ABCD, сторона якого дорівнює 12. На сторонах AD і BC квадрата вибрано точки K і M так, що AK = 4, MC = 3.

1 Визначте відстань між серединами відрізків AB і KM

2 Обчисліть довжину відрізка KM.

Впишіть відповіді:

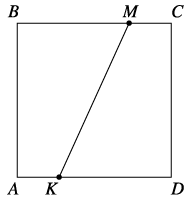
ABMK - трапеція з основами AK і BM (так як сторони AK і BM паралельні).
відстань між серединами відрізків AB і KM буде дорівнювати середній лінії трапеції
BM = BC - MC = 12 - 3 = 9
середня лінія = AK + BM2 = 4 + 92 = 6,5
з точки M проведемо перпендикуляр MN до AD
ND = MC = 3

MN = AB = 12

NK = AD - ND - AK = 12 - 4 - 3 = 5

Трикутник KNM прямокутний, тому за теоремою Піфагора

KM² = KN² + NM² = 12² + 5² = 144 + 25 = 169

KM = √169 = 13

Відео

Обчисліть значення похідної функції y = √13 - 3x у точці x₀ = 3.

Впишіть відповідь:

y ' = 12√13 - 3x·(13 - 3x)' = 12√13 - 3x·(-3) = -32√13 - 3x

y '(3) = -32√13 - 3·3 = -32√4 = -34 = -0,75

Відео

У готелі для проживання туристів є одномісні, двомісні та тримісні номери. Їх всього 124. Якщо всі номери в готелі заповнені, то одночасно в ньому проживає255 туристів. Скільки всього в цьому готелі тримісних номерів, якщо кількість одномісних номерів дорівнює кількості двомісних номерів?

Впишіть відповідь:

Нехай в готелі x - тримісних номерів та y -одномісних, тоді двомісних теж y.

З суми номерів в готелі маємо

x + 2y = 124

x = 124 - 2y

Тоді кількість туристів

3x + 2y + y = 255

3x + 3y = 255

x + y = 85

(124 - 2y) + y = 85

124 - 2y + y = 85

124 - y = 85

y = 124 - 85 = 39

x = 124 - 2y = 124 - 2·39 = 124 - 78 = 46

Відео

У прямокутній системі координат на площині задано паралелограм ABCD, cos A = 0,44. Визначте довжину діагоналі BD паралелограма якщо скалярний добуток векторів AB (6; -8) і AD дорівнює 88.

Впишіть відповідь:

|AB| = √6² + (-8)² = √36 + 64 = √100 = 10

AB · AD = |AB|·|AD|·cos A = 10·|AD|·0,44 = 4,4|AD| = 88

|AD| = 884,4 = 20

З трикутника ABD за теоремою косинусів

BD² = AB² + AD² - 2·AB·AD cos A = 10² + 20² - 2·10·20·0,44 = 100 +400 - 176 = 324

BD = √324 = 18

Відео

У чайному кіоску є лише розфасований у коробки по 100 г листовий чорний чай 8 видів, серед яких є вид "чорна перлина". Покупець вирішив придбати в цьому кіоску для подарункового набору три коробки чорного чаю трьох різних видів, серед яких обов'язково повинен бути вид "чорна перлина". Скільки всього в покупця є варіантів такого придбання трьох коробок чаю для набору з наявних у кіоску.

Впишіть відповідь:

Ми маємо обрати 3 різні сорти чаю з 8 серед яких, обов'язково повинен бути вид "чорна перлина"

Фактично ми відібрали один вид чаю "чорна перлина" і маємо обрати 2 різні сорти чаю з 7 сортів, що залишились.

Кількість вариантів буде дорівнювати кількості сполук з 7 по 2.

C 7 2 = 7!2!(7-2)! = 6·72 = 21

Відео

Побудуйте графік функції y = x² - x - 2|x + 1|. Користуючись графіком, визначте область значень цієї функції.

Це завдання вимагає розгорнуту відповідь, тому не може бути оцінено автоматично!

y = x² - x - 2|x + 1| = (x + 1)(x - 2)|x + 1|

ОДЗ x ≠ -1

Розкриємо модуль:

x > -1

y = (x + 1)(x - 2)x + 1 = x - 2 - це рівняння прямої

x < -1

y = (x + 1)(x - 2)-(x + 1) = -x + 2 - це рівняння прямої

Побудуємо графік

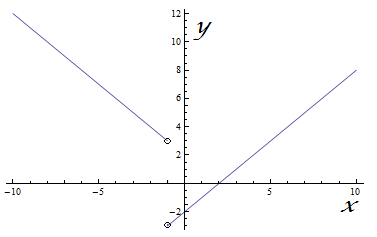
Область значень функції (-3; +∞)

Відео

Основою піраміди SABCD є ромб, більша діагональ якого AC = 30. Грань SBC є рівнобедреним трикутником (SB = SC) і перпендикулярна до площини основи піраміди. Ребро SC нахиено до площини основи піраміди під кутом 30°. Визначте кут між площинами (SAD) і (ABC), якщо виота піраміди дорівнює 5.

Це завдання вимагає розгорнуту відповідь, тому не може бути оцінено автоматично!

Намалюємо піраміду.

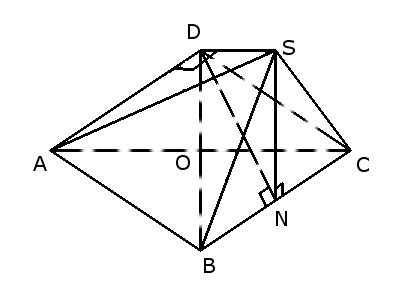
1) З точки S проведемо перпендикуляр SN до сторони BC.

Властивості перпендикулярних площин. Якщо пряма, яка лежить в одній із двох перпендикулярних площин, перпендикулярна до лінії їх перетину, то вона перпендикулярна і до другої площини.

Так як грань SBC⊥(ABC) SN⊥BC, то SN⊥(ABC), отже SN висота піраміди: SN = 5.

2) Кут між похилою та площиною — це кут між похилою та її проекцією на площині.

SN — перпендикуляр до площини ABC, SC — похила, NC — її проекція на площину АВС. Тому ∠SCN = 30°, як кут нахилу ребра CS до площини ABC

3) Трикутник SNC прямокутний, тому

CN = NS ctg ∠SCN = 5 ctg 30° = 5√3

Трикутник SBC рівнобедрений, тому його висота SN буде також і медіаною: CN = BN

CB = 2CN = 10√3

4) ABCD - ромб => AB = BC = CD = AD = 10√3

O - точка перетину діагоналей ромба ABCD.

AO = OC = AC/2 = 15

Так як діагоналі ромба перпендикулярні, то трикутник BOC прямокутний, тоді за теоремою Піфагора

OB² = BC² - OC² = (10√3)² - 15² = 300 - 225 = 75

OB = √75 = 5√3

BD = 2OB = 10√3

5) Трикутник BDC рівносторонній, так-як BD = DC = BC = 10√3 тому ∠DBC = 60°, DN - буде медіаною та вистою (DN⊥BC)

Трикутник BND прямокутний: DN = BD sin ∠DBC = 10√3 √32 = 15

6) Сторони ромба паралельни, отже, ND⊥AD.

SN — перпендикуляр до площини ABC, SD — похила, ND — її проекція на площину ABC. Тоді зо теоремою про три перпендикуляри SD⊥AD.

7) AD — пряма перетину площин SAD та ABC. ND⊥AD, SD⊥AD, тоді за означеням ∠SDN — кут між площинами SAD та ABC.

Трикутник SND прямокутний (∠SND=90°):

tg ∠SDN = SDND = 515 = 13

∠SDN = arctg 13

Відповідь: кут між площинами (SAD) і (ABC) дорівнює arctg 13.

Розв'яжіть рівняння √x² + (4a-4)x + 4a² - 2√2a5·5^2x - 5^{a + x} - 5^{a - 1} + 5^x = 0 залежно від значеня параметра a.

Це завдання вимагає розгорнуту відповідь, тому не може бути оцінено автоматично!

ОДЗ:
- a ≥ 0;
- Знаменник не може дорівнювати нулю, визначимо коли це можливо, розв'язавши рівняння
  
  5·5^2x - 5^{a + x} - 5^{a - 1} + 5^x = 0
  
  Зробимо заміну y = 5^x
  
  5y² - y5^a - 5^{a - 1} + y = 0
  
  5y² - (5^a - 1)y - 5^{a - 1} = 0
  
  Знайдемо дискримінант цього рівняння
  
  D = (5^a - 1)² - 4·5·(-5^{a - 1}) = 5^2a - 2·5^a + 1 + 4·5^a = 5^2a + 2·5^a + 1 = (5^a + 1)²
  
  y = 5^a - 1 ± (5^a + 1)10
  
  тоб-то
  
  5^x = 5^a - 1 + 5^a + 110 = 5^{a - 1} => x = a - 1
  
  або
  
  5^x = 5^a - 1 - 5^a - 110 = -15 < 0, що неможливо, бо 5^x > 0
  
  Отже знаменник рівний нулю, коли x = a - 1.
- x² + (4a-4)x + 4a² ≥ 0;
Корені рівняння потрібно шукати серед коренів рівняння

√x² + (4a-4)x + 4a² - 2√2a = 0

√x² + (4a-4)x + 4a² = 2√2a

x² + (4a-4)x + 4a² = 4(2a)

N.B. Так як з першої умови ОДЗ a ≥ 0, то попереднє рівняння гарантує виконання третьої умова з ОДЗ x² + (4a - 4)x + 4a² ≥ 0

x² + (4a - 4)x + 4a² - 8a = 0

D = (4a - 4)² - 4(4a² - 8a) = 16a² - 32a + 16 - 16a² + 32a = 16

D > 0, отже, при a ≥ 0 рівняння має два різних корені:

x = 4 - 4a ± √162 = 2 - a ± 2

x₁ = 4 - 2a

x₂ = -2a
Пам'ятаємо з ОДЗ, що x ≠ a − 1, тому:
якщо x₁ = 4 - 2a = a − 1, тоб-то 3a = 5 => a = 53, то маємо один корінь x₂ = -2a = -103 = -313

якщо x₂ = -2a = a − 1, тоб-то 3a = 1 => a = 13, то маємо один корінь x₁ = 4 - 2a = 4 - 23 = 313

Відповідь:

Якщо a∈(−∞; 0), то корені відсутні.

Якщо a∈[0; 13)∪(13; 53)∪(53; +∞), то рівняння має два корені
x₁ = 4 - 2a та x₂ = -2a

Якщо a = 13, то рівняння має один корінь x = 313.

Якщо a = 53, то рівняння має один корінь x = -313.

Ви не виконали всі завдання!
Ви впевнені, що бажаєте завершити тестування?

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!

загальна кількості книжок	-	100%
кількість підручників	-	12%

кількісті довідників	-	8%
загальна кількості книжок	-	100%