OnlineMSchool
Вивчення математики онлайн.
Вивчайте математику з нами і переконайтесь: "Математика - це просто!"
Реєстрація Увійти Вийти

Коло, круг, сегмент, сектор. Формули та властивості кола

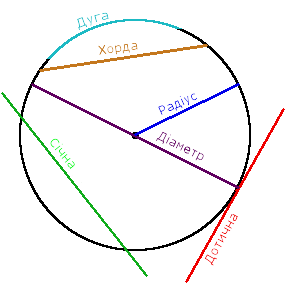
Зображення кола, радіуса, діаметра, хорди, дуги, січної та дотичної Зображення сектора і сегмента Зображення центрального і вписанного кута

Означення. Коло — це сукупність усіх точок на площині, які знаходяться на однаковій відстані від заданої точки О, яка називається центром кола.
Означення. Одиничне коло - коло, радіус якого дорівнює одиниці.
Означення. Круг - частина площини, обмежена колом.
Означення. Радіус кола R - відстань від центра кола О до будь-якої точки кола.
Означення. Діаметр кола D - відрізок, який сполучає дві точки кола та проходить через його центр.

Основні властивості кола

1. Діаметр кола дорівнює двом радіусам.

D = 2r

2. Найкоротша відстань від центра кола до січної (хорди) завжди менша радіуса.
3. Через три точки, які не лежать на одній прямій, можна провести тільки одне коло.
4. Серед всіх замкнених кривих з однаковою довжиною, коло має найбільшу площу.
5. Якщо два кола дотикаються в одній точці, то ця точка лежить на прямій, що проходить через центри цих кіл.

Формули довжини кола та площі круга

Формули довжини кола

1. Формула довжини кола через діаметр:

L = πD

2. Формула довжини кола через радіус:

L = 2πr

Формули площі круга

1. Формула площі круга через радіус:

S = πr2

2. Формула площі круга через діаметр:

S = πD24

Рівняння кола

1. Рівняння кола з радіусом r та центром у початку декартової системи координат:

r2 = x2 + y2

2. Рівняння кола з радіусом r та центром у точці з координатами (a, b) в декартовій системи координат:

r2 = (x - a)2 + (y - b)2

3. Параметричне рівняння кола з радіусом r та центром у точці з координатами (a, b) в декартовій системи координат:
{x = a + r cos t
y = b + r sin t

Дотична до кола та її властивості

Означення. Дотична до кола - пряма, яка дотикається до кола тільки в одній точці.

Основні властивості дотичних до кола

1. Дотична завжди перпендикулярна до радіуса кола, проведеного до точки дотику.
2. Найкоротша відстань від центра кола до дотичної дорівнює радіусу кола.
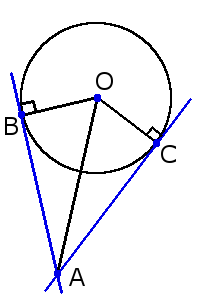
дотична
3. Якщо дві дотичні, з точками дотику B та C, на одному колі не паралельні, то вони перетинаються в точці A, а відрізок між точкою дотику та точкою перетину однієї дотичної дорівнює такому ж відрізку на іншій дотичній:

AB = AC

Також, якщо провести пряму через центр кола О та точкою перетину A цих дотичних, то кут утворений між однією дотичною і цією прямою, буде дорівнювати куту між іншою дотичною та цією прямою:

∠ОAС = ∠OAB

Січна кола та її властивості

Означення. Січна кола - пряма, яка сполучає дві точки кола.

Основні властивості січних

Січна
1. Якщо з точки поза колом (Q) виходять дві січні, які перетинають коло у двох точках A і B для однієї січної та C і D для іншої січної, то добутки відрізків двох січних рівні між собою:

AQ ∙ BQ = CQ ∙ DQ

Січна
2. Якщо з точки поза колом Q виходить січна, що перетинає коло у двох точках A і B, та дотична з точкою дотику C, то добуток відрізків січної дорівнює квадрату довжини відрізка дотичної:

AQ ∙ BQ = CQ2

Хорда кола її довжина та властивості

Означення. Хорда кола - відрізок, який сполучає дві точки кола.

Довжина хорди

довжина хорди через центральний кут
1. Довжина хорди через центральний кут та радіус:

AB = 2r sin α2

довжина хорди через вписаний кут
2. Довжина хорди через вписаний кут та радіус

AB = 2r sin α

Основні властивості хорд

хорди
1. Дві однакові хорди стягують дві однакові дуги

якщо хорди AB = CD, то

дуги ◡ AB = ◡ CD

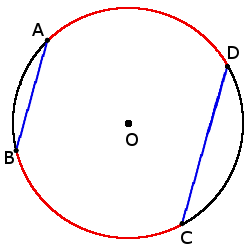
хорди
2. Якщо хорди паралельні, то дуги між ними будуть однакові:

якщо хорди AB ∣∣ CD, то

◡ AD = ◡ BC

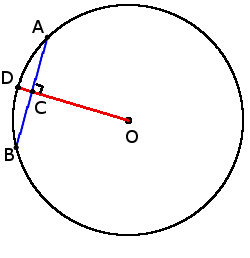
хорди
3. Якщо радіус кола перпендикулярний до хорди, то він розділяє хорду навпіл у точці їх перетину:

якщо OD ┴ AB, то

AC = BC

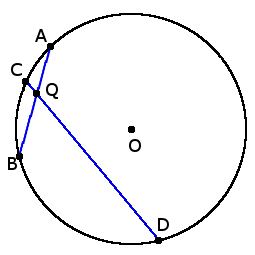
хорди
4. Якщо дві хорди AB та CD перетинаються в точці Q, то добуток відрізків, що утворилися при перетині, однієї хорди дорівнюють добутку відрізків іншої хорди:

AQ ∙ BQ = DQ ∙ QC

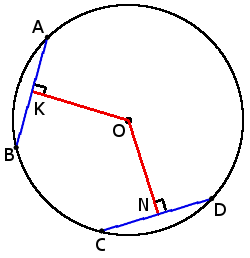
хорди
5. Хорди з однаковою довжиною знаходяться на однаковій відстані від центра кола.

якщо хорди AB = CD, то

ON = OK

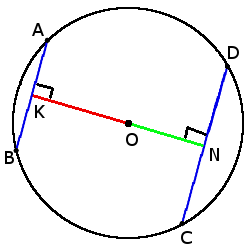
хорди
6. Чим більша хорда тим ближче вона до центру.

якщо CD > AB, то

ON < OK

Центральний кут, вписаний кут та їх властивості

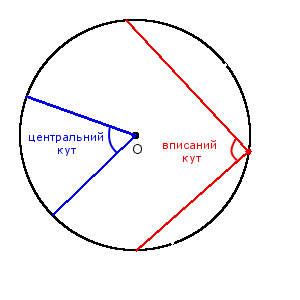
Означення. Центральний кут кола - кут, вершиною якого є центр кола.
Означення. Кут вписаний в коло - кут, вершина якого лежить на колі, а сторони кута перетинають коло.

Основні властивості кутів

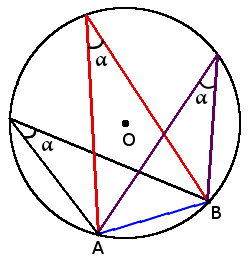
вписані кути, що спираються на одну дугу
1. Всі вписані кути, які спираються на одну дугу - рівні.

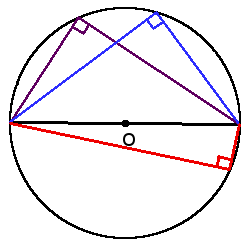
вписаний кут, який спирається на діаметр
2. Вписаний кут, який спирається на діаметр кола буде прямим (90°).

вписаний та центральний кут
3. Вписаний кут дорівнює половині центрального кута, що спирається на ту саму дугу

β = α2

вписані кути, які спираються на одну хорду
4. Якщо два вписані кути спираються на одну хорду та знаходяться по різні сторони від неї, то сума цих кутів дорівнює 180°

α + β = 180°

Означення. Дуга кола (◡) - частина кола, яка сполучає дві точки на колі.
Означення. Градусна міра дуги - кут між двома радіусами, які обмежують цю дугу. Градусна міра дуги завжди дорівнює градусній мірі центрального кута, який обмежує цю дугу своїми сторонами.
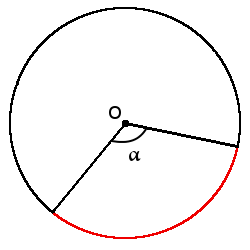
довжина дуги
Формула довжини дуги через центральний кут (в градусах):

l = πr180°∙ α

Означення. Півколо - дуга у якої кінці сполучені діаметром кола.
Означення. Півкруг (◓) - частина круга, яка обмежена півколом та діаметром.
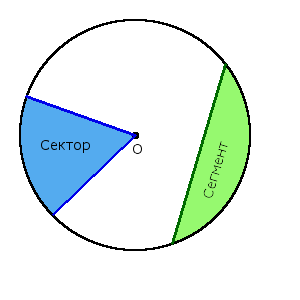
Означення. Сектор (◔) - частина круга, яка обмежена двома радіусами та дугою між цими радіусами.
сектор
Формула. Формула площі сектора через центральний кут (в градусах)

S = πr2360°∙ α

Означення. Сегмент - частина круга, яка обмежена дугою та хордою, що сполучає її кінці.
Означення. Концентричні кола - кола з різними радіусами які мають спільний центр.
Означення. Кільце - частина площини обмежена двома концентричними колами.
Формули з геометрії Трикутник. Формули та властивості трикутника Квадрат. Формули та властивості квадрату Прямокутник. Формули та властивості прямокутника Паралелограм. Формули та властивості паралелограма Ромб. Формули та властивості ромба Трапеція. Формули та властивості трапеції - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції - Прямокутна трапеція. Формули та властивості прямокутної трапеції Правильний многокутник. Формули і властивості правильного многокутника Коло, круг, сегмент, сектор. Формули та властивості Еліпс. Формули та властивості еліпса Куб. Формули та властивості куба Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду Призма. Формули, ознаки та властивості Піраміда. Формули та властивості піраміди Сфера, куля, сегмент та сектор. Формули та властивості Циліндр. Формули та властивості циліндра Конус. Формули та властивості конуса Формули площі геометричних фігур S Формули периметра геометричних фігур P Формули об'єму геометричних фігур V Формули площі поверхні геометричних фігур S
Всі таблиці і формули

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!

0
Приєднуйтесь до нас