OnlineMSchool
Вивчення математики онлайн.
Вивчайте математику з нами і переконайтесь: "Математика - це просто!"
Реєстрація Увійти Вийти

Призма. Формули, ознаки та властивості призми

Навігація по сторінці: Визначення призми Елементи призми Пряма призма Похила призма Правильна призма Зрізана призма Об'єм призми Площа поверхні призми Основні властивості призми
Означення.
Призма — це багатогранна об'ємна фігура, яка складається з двох однакових плоских багатокутників (основ), що знаходяться в двох паралельних площинах, а інші грані (бокові грані) - паралелограми, що мають спільні сторони з цим багатокутником.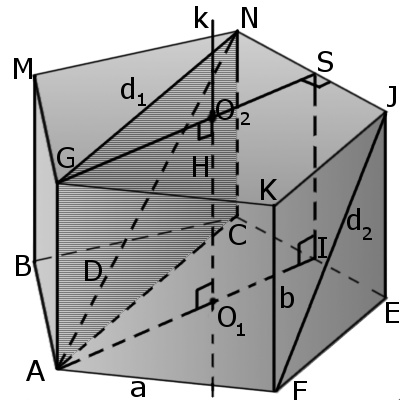
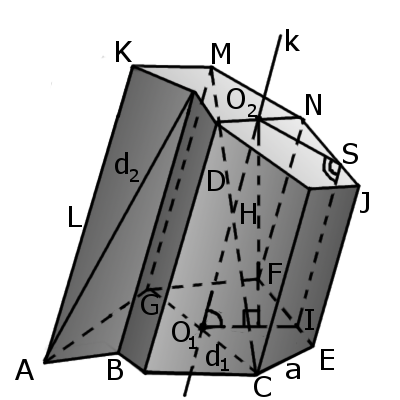Зображення призми з позначеннями Зображення призми з позначеннями
Рис.1 Рис.2

Означення. Основи призми - дві грані, які є паралельними плоскими багатокутниками (ABCEF, GMNJK).
Означення. Бічні грані призми - всі інші грані за винятком основ.
Означення. Бічна поверхня призми - сукупність всіх бічних граней призми.
Означення. Поверхня призми - це сукупність поверхонь двох основ та бічної поверхні.
Означення. Бокове ребро призми - спільна сторона двох бічних граней.
Означення. Висота - це перпендикуляр (H), який з'єднує дві основи призми.
Означення. Діагональ основи призми (AC) - це відрізок, який з'єднує дві не сусідні вершини, що належать ці й же основі.
Означення. Діагональ бічної грані призми (FJ) - це відрізок, який з'єднує дві протилежні вершини, що лежать на одній бічній грані проте належать різним основам.
Означення. Діагональ призми (AN) - це відрізок, який з'єднує дві вершини, що лежать на різних основах, але не лежать на одній бічній стороні.
Означення. Діагональний перетин - це перетин призми площиною, яка проходить через діагональ основи призми та бічне ребро. Трикутна призма (в основі призми трикутники) не має діагональних перетинів.
Означення. Перпендикулярний перетин - це перетин призми площиною, яка перетинає бічні ребра призми під прямим кутом.
Означення. Пряма призма - це призма у якої всі бічні грані перпендикулярні до основи. Висота дорівнює довжині ребра.
Означення. Похила призма - це призма у якої бічні грані не перпендикулярні до основи.
Означення. Правильна призма - це призма у якої дві основи є правильними багатокутниками. Правильна призма може бути як прямою так і похилою.
Означення. Зрізана призма - це призма у якої дві основи не паралельні (рис. 2). Зрізана призма може бути як правильною так і прямою чи похилою.

Об'єм призми

Формула. Об'єм призми через площу основи та висоту:

V = SоснH

Формула. Об'єм похилої призми через площу перпендикулярного перерізу та довжину бычного ребра:

V = SпL

Формула. Об'єм правильної прямої призми через висоту, довжину сторони та кількість мторін:
V = nha2ctgπ
4n

Площа поверхні призми

Формула.Площа бічної поверхні призми через периметр основи та висоту:

Sb = P·h

Формула. Площа поверхні призми через площу основи, периметр основи та висоту:

S = 2Soсн + P·h

Формула. Площа поверхні правильної призми через висоту, довжину сторони та кількість сторін:
S = na2ctgπ + nah
2n

Основні властивості призми

Основи призми - рівні багатокутники.
Бічні грані призми - паралелограми.
Бічні ребра призми паралельні та рівні між собою
Перпендикулярний перетин перпендикулярний до всіх бічних ребер
Перпендикулярний перетин перпендикулярний до всіх бічних граней
Висота прямої призми дорівнює довжині ребра.
Висота похилої призми завжди менша довжини ребра.
В прямої призми гранями можуть бути прямокутники та квадрати.
Формули з геометрії Трикутник. Формули та властивості трикутника Квадрат. Формули та властивості квадрату Прямокутник. Формули та властивості прямокутника Паралелограм. Формули та властивості паралелограма Ромб. Формули та властивості ромба Трапеція. Формули та властивості трапеції - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції - Прямокутна трапеція. Формули та властивості прямокутної трапеції Правильний многокутник. Формули і властивості правильного многокутника Коло, круг, сегмент, сектор. Формули та властивості Еліпс. Формули та властивості еліпса Куб. Формули та властивості куба Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду Призма. Формули, ознаки та властивості Піраміда. Формули та властивості піраміди Сфера, куля, сегмент та сектор. Формули та властивості Циліндр. Формули та властивості циліндра Конус. Формули та властивості конуса Формули площі геометричних фігур S Формули периметра геометричних фігур P Формули об'єму геометричних фігур V Формули площі поверхні геометричних фігур S
Всі таблиці і формули

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!

0
Приєднуйтесь до нас