Піраміда. Формули та властивості піраміди

Навігація по сторінці: Визначення піраміди Єлементи піраміди Об'єм та площа поверхні піраміди Властивості піраміди Зв'язок піраміди зі сферою, конусом та циліндром Види пірамід

Означення.

Піраміда — це багатогранна об'ємна фігура, яка обмежена плоским багатокутником (основа), та трикутниками, що мають спільну вершину, яка не лежить в площині основи.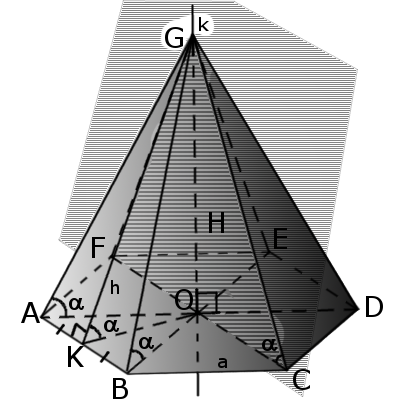

Рис.1

Означення. Бічна грань - це трикутник у яких один кут лежить на вершині піраміди, а протилежна йому сторона, є стороною основи (багатокутника).

Означення. Бічні ребра - спільні сторони бічних граней. У піраміди стільки ребер скільки кутів у багатокутника.

Означення. Висота піріміди - це перпендикуляр, опущений з вершини на основу піраміди.

Означення. Апофема - це перпендикуляр бічної грані піраміди, опущений з вершини піраміди до сторони основи.

Означення. Діагональний перетин - це перетин піраміди площиною, яка проходить через вершину піраміди та діагональ основи.

Означення. Правильна піраміда - це піраміда у якої основою є правльний багатокутник, а висота опускається в центр основи.

Об'єм та площа поверхні піраміди

Формула. Об'єм піраміди через площу основу та висоту:

V =	1	S_оснH
	3

Означення. Бічна поверхня піраміди - це сукупна площа всіх бокових граней піраміди.

Означення. Повна поверхня піраміди - це сукупність площ бічної поверхні та основи піраміди.

Формула. Площа бічної поверхні правильної піраміди через периметр основи та апофему:

S_b =	1	ph
	2

Для визначення площі основи піраміди дивіться формули площі плоских фігур

Для визначення площі основи равильної піраміди дивіться формули площі правильних многокутників

Властивості піраміди

Якшо всі бічні ребра рівні, то навколо основи піраміди можна описати коло, та вершина піраміди проецюється в його центр.

Якшо всі бічні ребра рівні, то бічні ребра утворюють з площиною основи рівні кути.

Бічні ребра рівні, якщо бічні ребра утворюють з площиною основи рівні кути або якщо навколо основи піраміди можна описати коло та вершина піраміди проецюється в його центр.

Якшо бічні грані нахилені до площини основи під одним кутом, то в основу піраміди можна вписати коло, та вершина пірамиди проецюється в його центр.

Якшо бічні грані нахилені до площини основи під одним кутом, то высоти бічих граней рівні.

Властивості правильної піраміди

1. Вершина піраміди однаково віддалені від усіх кутів основи.

2. Всі бічні ребра рівні.

3. Всі бічні ребра нахилені під однаковим кутом до основи.

4. Апофеми всіх бічних граней рівні.

5. Площі всіх бічних граней рівні.

6. Всі грані мають однакові двогранні (плоскі) кути.

7. Навколо піраміди можна описати сферу. Центром описаної сфери буде точка перетину перпендикулярів, які проходять через середину ребер.

8. В піраміду можна вписати сферу. Центром вписаної сфери буде точка перетину бісектрис, які виходять з кута між ребром та основою.

9. Якщо центр вписаної сфери співпадає з центром описаної сфери, то сума плоских кутів при вершині дорівнює π, або один кут дорівнює π/n, де n - це кількість кутів в основі піраміди.

Зв'язок піраміди зі сферою

Навколо піраміди можна описати сферу тоді, коли в основі пірамиди лежить многкутник, навколо якого можна описати коло (необхідна і достатня умова). Центром сфери будет точка перетину площин, що проходять через середини бічних ребер піраміди перпендикулярно до них.

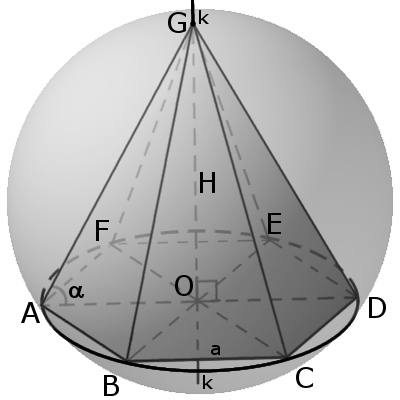
Навколо будьякої трикутної або правильної піраміди завжди можна описати сферу.

В піраміду можна вписати сферу, якщо бісекторні площини внутрішніх двогранних кутів піраміди перетинаються в одній точці (необхідна і достатня умова). Ця точка буде центром сфери.

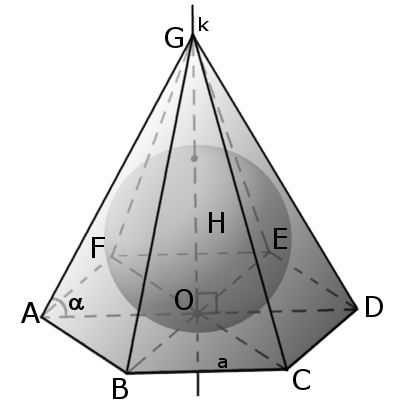
Зв'язок піраміди з конусом

Конус називається вписаним в піраміду, якщо їх вершини співпадають, а його основа вписана в основу піраміди.

Конус можна вписати в пирамиду, якщо апофеми піраміди рівні між собою.

Конус называється описаним навколо піраміди, якщо їх вершини співпадають, а його основа описана навколо основи піраміди.

Конус можна описати навколо піраміди якщо, всі бічні ребра піраміди рівні між собою.

Зв'язок піраміди з циліндром

Циліндр называється описаним навколо піраміди, якщо вершина піраміди лежить но одій основі циліндра, а друга основа циліндра описана навколо основи піраміди.

Цилиндр можна описати навколо піраміди якщо, навколо основи піраміди можна описати коло.

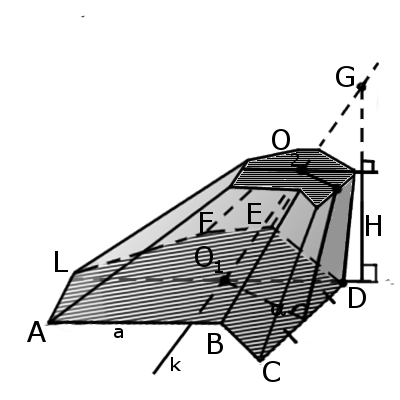Означення. Зрізана піраміда (пірамідальна призма) - це багатогранник, який знаходиться між основою піраміди та площиною перетину, паралельною до основи. Таким чином піраміда має більшу основу та меншу основу, яка подібна до більшої. Бічні грані є трапеції.

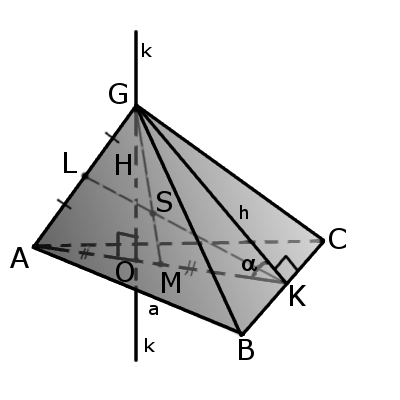
Означення. Тикутна піраміда (чотиригранник) - це піраміда у якої грані та основа є довільними трикутниками.

У чотиригранника чотири грані та чотири вершини і шість ребер, де будь-які два ребра не мають спільних вершин та не дотикаються.

Кожна вершина складається з трьох граней та ребер, які утворюють тригранний кут.

Відрізок, який сполучає вершину чотиригранника з центром протилежної грані називається медіаною чотиригранника.

Бімедіаною називається відрізок, який сполучає середини протилежних ребер, що не дотикаються.

Всі бімедіани та медіани чотиригранника перетинаються в одній точці. При цьому бімедіани діляться навпіл, а медіани у відношенні 3:1 починаючи з вершини.

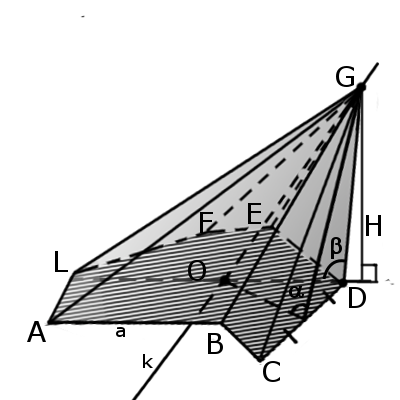Означення. Похила піраміда - це піраміда у якої одне з ребер утворює тупий кут з основою.

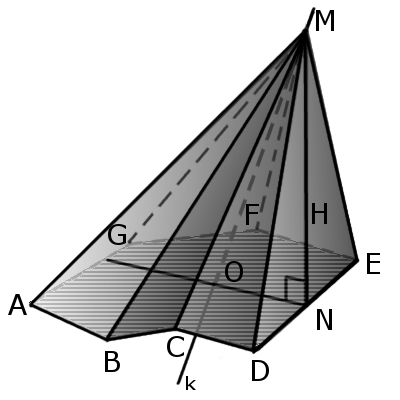Означення. Прямокутна піраміда - це піраміда у якої одне з бічних ребер перпендикулярне до основи.

Означення. Гострокутна піраміда - це піраміда у якої апофема більша за половину довжини сторони основи.

Означення. Тупокутна піраміда - це піраміда у якої апофема менша за половину довжини сторони основи.

Означення. Правльний тетраедр - чотиригранник у якого всі чотири грані - рівносторонні трикутники. Він є одним із п'яти правильних багатокутників. У правильного тетраедра всі двогранні кути (між гранями) та тригранні кути (при вершині) рівні.

Означення. Прямокутний тетраедр називається чотиригранник у якого прямий кут між трьома ребрами при вершині (ребра перпендикулярні). Три грані, що утворюють такий прямокутний тригранний кут, є прямокутними трикутниками, а основа довільним трикутником. Апофема будь-якої грані дорівнює половині строни основи, на яку падає апофема.

Означення. Рівногранний тетраедр називається чотиригранник у якого бічні грані рівні між собою, а основа - правильний трикутник. У такого тетраедра грані це рівнобедрені трикутники.

Означення. Ортоцентричний тетраедр називається чотиригранник у якого всі висоти (перпендикуляри), що опущені з вершини до протилежної грані, перетинаються в одній точці.

Означення. Зіркова піраміда називається багатогранник у якого основою є зірка.

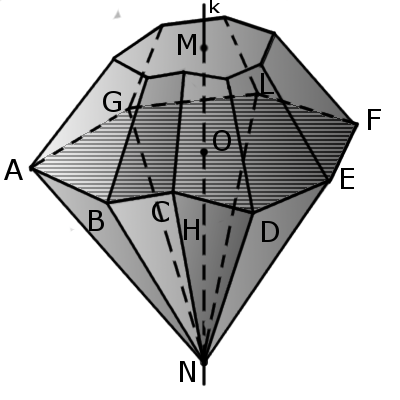Означення. Біпіраміда - багатогранник, який складається з двох різних пірамід (також можуть бути зрізані піраміди), що мають спільну основу, а вершини лежать по різні сторони від площини основи.

Формули з геометрії Трикутник. Формули та властивості трикутника