Ромб. Формули, ознаки та властивості ромба

Навігація по сторінці: Означення ромба Ознаки ромба Основні властивості ромба Сторони ромба Діагоналі ромба Периметр ромба Площа ромба Коло, вписане в ромб

Означення.

Ромб — це паралелограм, який має рівні сторони. Якщо у ромба всі кути прямі, тоді він називається квадратом.

Ромби відрізняються між собою за сторонами та кутами.


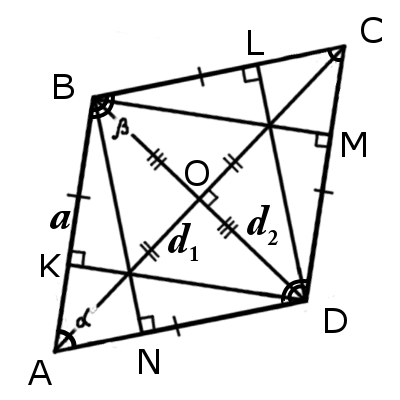
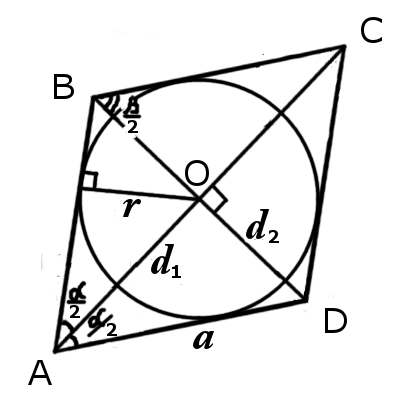
Рис.1		Рис.2

Ознаки ромба

Паралелограм ABCD буде ромбом, якщо виконується хоча б одна із наступних умов:

1. Дві його суміжні сторони рівні (звідси випливає, що всі сторони рівні):

АВ = ВС = СD = AD

2. Його діагоналі перетинаються під прямим кутом:

AC┴BD

3. Одна із діагоналей (бісектриса) ділить кути навпіл:

∠BAC = ∠CAD або ∠BDA = ∠BDC

4. Якщо всі висоти рівні:

BN = DL = BM = DK

5. Якщо діагоналі ділять паралелограм на чотири рівні прямокутні трикутники:

Δ ABO = Δ BCO = Δ CDO = Δ ADO

6. Якщо в паралелограм можна вписати круг.

Основні властивості ромба

1. Має всі властивості паралелограма

2. Діагоналі перпендикулярні:

AC┴BD

3. Діагоналі є бісектрисами кутів ромба:

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

4. Сума квадратів діагоналей рівна квадрату сторони, помноженому на чотири:

AC² + BD² = 4AB²

5. Точка перетину діагоналей називається центром симетрії ромба.

6. В будь-який ромб можна вписати коло.

7. Центром кола, вписаного в ромб, буде точка перетину його діагоналей.

Сторона ромба

Формули визначення довжини сторони ромба:

1. Формула сторони ромба через площу і висоту:

a =	S
	h_a

2. Формула сторони ромба через площу і синус кута:

a =	√S
	√sinα

a =	√S
	√sinβ

3. Формула сторони ромба через площу і радіус вписаного кола:

a =	S
	2r

4. Формула сторони ромба через дві діагоналі:

a =	√d₁² + d₂²
	2

5. Формула сторони ромба через діагональ і косинус гострого кута (cos α) або косинус тупого кута (cos β):

a =	d₁
	√2 + 2 cosα

a =	d₂
	√2 - 2 cosβ

6. Формула сторони ромба через більшу діагональ і половинний кут:

a =	d₁
	2cos(α/2)

a =	d₁
	2sin(β/2)

7. Формула сторони ромба через малу діагональ і половинний кут:

a =	d₂
	2cos(β/2)

a =	d₂
	2sin(α/2)

8. Формула сторони ромба через периметр:

a =	Р
	4

Діагоналі ромба

Означення.

Діагональ ромба - це довільний відрізок, що з'єднує дві вершини протилежних кутів ромба.

Ромб має дві діагоналі - більшу d₁, та меншу - d₂

Формули визначення довжини діагоналі ромба:

1. Формули більшої діагоналі ромба через сторону і косинус гострого кута (cosα) або косинус тупого кута (cosβ)

d₁ = a√2 + 2 · cosα

d₁ = a√2 - 2 · cosβ

2. Формули меншої діагоналі ромба через сторону і косинус гострого кута (cosα) або косинус тупого кута (cosβ)

d₂ = a√2 + 2 · cosβ

d₂ = a√2 - 2 · cosα

3. Формули більшої діагоналі ромба через сторону і половинний кут:

d₁ = 2a · cos(α/2)

d₁ = 2a · sin(β/2)

4. Формули меншої діагоналі ромба через сторону і половинний кут:

d₂ = 2a · sin(α/2)

d₂ = 2a · cos(β/2)

5. Формули діагоналей ромба через сторону і другу діагональ:

d₁ = √4a² - d₂²

d₂ = √4a² - d₁²

6. Формули діагоналей через тангенс гострого tgα або тупого tgβ кута і другу діагональ:

d₁ = d₂ · tg(β/2)

d₂ = d₁ · tg(α/2)

7. Формули діагоналей через площу і другую діагональ:

d₁ =	2S
	d₂

d₂ =	2S
	d₁

8. Формули діагоналей через синус половинного кута і радіус вписаного кола:

d₁ =	2r
	sin(α/2)

d₂ =	2r
	sin(β/2)

Периметр ромба

Означення.

Периметром ромба називається сума довжин всіх сторін ромба.

Довжину сторони ромба можна знайти за формулами, вказаними вище.

Формула визначення довжини периметра ромба:

Формула периметра ромба через сторону ромба:

P = 4a

Площа ромба

Означення.

Площа ромба - це простір, обмежений сторонами ромба, тобто в межах периметра ромба.

Формули визначення площі ромба:

1. Формула площі ромба через сторону і висоту:

S = a · h_a

2. Формула площі ромба через сторону і синус будь-якого кута:

S = a² · sinα

3. Формула площі ромба через сторону і радіус:

S = 2a · r

4. Формула площі ромба через дві діагоналі:

S =	1	d₁d₂
	2

5. Формула площі ромба через синус кута і радіус вписаного кола:

S =	4r²
	sinα

6. Формули площі через більшу діагональ і тангенс гострого кута (tgα) або малу діагональ і тангенс тупого кута (tgβ):

S =	1	d₁² · tg(α/2)
	2

S =	1	d₂² · tg(β/2)
	2

Коло, вписане у ромб

Означення.

Колом, вписаним у ромб, називається коло, що дотикається до всіх сторін ромба та має центр на перетині діагоналей ромба.

Формули визначення радіуса кола, вписаного в ромб:

1. Формула радиуса кола, вписаного в ромб, через висоту ромба:

r =	h
	2

2. Формула радіуса кола, вписаного в ромб, через площу та сторону ромба:

r =	S
	2a

3. Формула радіуса кола, вписаного в ромб, через площу та синус кута:

r =	√S · sinα
	2

4. Формули радіуса кола, вписаного в ромб, через сторону і синус будь-якого кута:

r =	a · sinα
	2

r =	a · sinβ
	2

5. Формули радіуса кола, вписаного в ромб, через діагональ та синус кута:

r =	d₁ · sin(α/2)
	2

r =	d₂ · sin(β/2)
	2

6. Формула радіуса кола, вписаного в ромб, через дві діагоналі:

r =	d₁ · d₂
	2√d₁² + d₂²

7. Формула радіуса кола, вписаного в ромб, через дві діагоналі та сторону:

r =	d₁ · d₂
	4a

Формули з геометрії Трикутник. Формули та властивості трикутника

Квадрат. Формули та властивості квадрату

Прямокутник. Формули та властивості прямокутника

Паралелограм. Формули та властивості паралелограма

Ромб. Формули та властивості ромба

Трапеція. Формули та властивості трапеції

- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції

- Прямокутна трапеція. Формули та властивості прямокутної трапеції

Правильний многокутник. Формули і властивості правильного многокутника

Коло, круг, сегмент, сектор. Формули та властивості

Еліпс. Формули та властивості еліпса

Куб. Формули та властивості куба

Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду Призма. Формули, ознаки та властивості

Піраміда. Формули та властивості піраміди

Сфера, куля, сегмент та сектор. Формули та властивості

Циліндр. Формули та властивості циліндра

Конус. Формули та властивості конуса

Формули площі геометричних фігур S Формули периметра геометричних фігур P Формули об'єму геометричних фігур V Формули площі поверхні геометричних фігур S

Всі таблиці і формули

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!