Основні властивості коренів.
Означення
Корнем n-того степеня із числа a називається таке число b, n-та степінь якого рівна a
Для a > 0 і b > 0 і натуральних чисел n, m, k виконуються наступні співвідношення:
- n√a b = n√a · n√b
- $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$
- $(\sqrt[n]{a})^k=\sqrt[n]{a^k}$
- $\sqrt[n]{\sqrt[m]{a}}=\sqrt[nm]{a}$
- $\sqrt[nk]{a^k}=\sqrt[n]{a}$
- $\sqrt[n·k]{a^{m·k}}=(\sqrt[n]{a^m})$
$\sqrt[n]{a^n}=$ 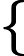
|a| якщо n – парне a якщо n – непарне - для довільних a і b, таких що 0 ≤ a ≤ b справедлива нерівність:
n√ a ≤ n√ b
Формули скороченого множення (a ± b)2
Формули і властивості степенів an
Формули і властивості корнів n√a
Формули і властивості логарифмів loga b
Формули і властивості арифметичної прогресії an
Формули і властивості геометричної прогресії bn
Тригонометричні формули sin x cos x
Обернені тригонометричні формули arcsin x
Таблиця похідних d dx
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
