Рівнобічна трапеція. Формули, ознаки та властивості рівнобічної трапеції
Навігація по сторінці:
Означення рівнобічної трапеції
Ознаки рівнобічної трапеції
Основні властивості рівнобічної трапеції
Сторони рівнобічної трапеції
Середня лінія рівнобічної трапеції
Висота рівнобічної трапеції
Діагоналі рівнобічної трапеції
Площа рівнобічної трапеції
Коло описане навколо рівнобічної трапеції
Означення.
Рівнобічна трапеція — це трапеція, у якої бокові сторони рівні.На цій сторінці представлені формули, що характерні рівнобічній трапеції. Не забувайте, що для рівнобічної трапеції виконуються всі формули та властивості трапеції.
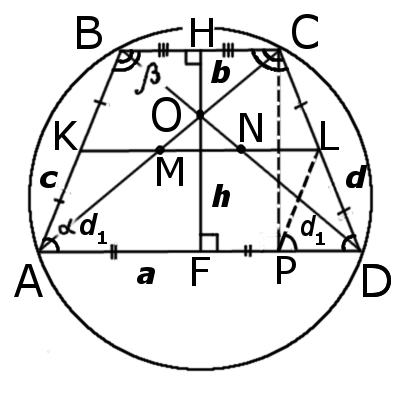 |
| Рис.1 |
Ознаки рівнобічної трапеції
Трапеція буде рівнобічною, якщо виконується одна із цих умов:1. Кути при основі рівні:
∠ABC = ∠BCD і ∠BAD = ∠ADC
2. Діагоналі рівні:
AC = BD
3. Однакові кути між діагоналями і основами:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сума протилежних кутів дорівнює 180°:
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Навколо трапеції можна описати коло
Основні властивості рівнобічної трапеції
1. Сума кутів прилеглих до бокової сторони рівнобічної трапеції дорівнює 180°:
∠ABC + ∠BAD = 180° і ∠ADC + ∠BCD = 180°
2. Якщо в рівнобічну трапецію можна вписати коло, то бокова сторона дорівнює середній лінії трапеції:
AB = CD = m
3. Навколо рівнобічної трапеції можна описати коло
4. Якщо діагоналі взаємно перпендикулярні, то висота дорівнює півсумі основ (середній лінії):
h = m
5. Якщо діагоналі взаємно перпендикулярні, то площа трапеції дорівнює квадрату висоти:
SABCD = h2
6. Якщо в рівнобічну трапецію можна вписати коло, то квадрат висоти рівний добутку основ трапеції:
h2 = BC · AD
7. Сума квадратів діагоналей дорівнює сумі квадратів бокових сторін плюс подвоєному добутку основ трапеції:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
8. Пряма, що проходить через середини основ, перпендикулярна основам і являється віссю симетрії трапеції:
HF ┴ BC, HF ┴ AD
9. Висота (CP), опущена із вершини (C) на більшу основу (AD), ділить її на більший відрізок (AP), який дорівнює півсумі основ та менший (PD) - дорівнює піврізниці основ:
| AP = | BC + AD |
| 2 |
| PD = | AD - BC |
| 2 |
Сторони рівнобічної трапеції
Формули довжин сторін рівнобічної трапеції:
1. Формули довжин сторін через інші сторони, висоту та кут:
a = b + 2h ctg α = b + 2c cos α
b = a - 2h ctg α = a - 2c cos α
| c = | h | = | a - b |
| sin α | 2 cos α |
2. Формула довжини сторін трапеції через діагоналі та інші сторони:
| a = | d12 - c2 | b = | d12 - c2 | c = √d12 - ab |
| b | a |
3. Формули довжини основ через площу, висоту та іншу основу:
| a = | 2S | - b b = | 2S | - a |
| h | h |
4. Формули довжини бокової сторони через площу, середню лінію та кут при основі:
| с = | S |
| m sin α |
5. Формули довжини бокової сторони через площу, основи та кут при основі:
| с = | 2S |
| (a + b) sin α |
Середня лінія рівнобічної трапеції
Формули довжини середньої лінії рівнобічної трапеції:
1. Формула визначення довжини середньої лінії через основи, висоту та кут при основі:
m = a - h ctg α = b + h ctg α = a - √c2 - h2 = b + √c2 - h2
2. Формула середньої лінії трапеції через площу та сторону:
| m = | S |
| c sin α |
Висота рівнобічної трапеції
Формули визначення довжини висоти рівнобічної трапеції:
1. Формула висоти через сторони:
| h = | 1 | √4c2 - (a - b)2 |
| 2 |
2. Формула висоти через сторони та кут прилеглий до основи:
| h = | a - b | tg β | = c sin β |
| 2 |
Діагоналі рівнобічної трапеції
Діагоналі рівнобічної трапеції рівні:
d1 = d2
Формула довжини діагоналей рівнобічної трапеції:
1. Формула довжини діагоналі через сторони:
d1 = √с2 + ab
2. Формули довжини діагоналі по теоремі косинусів:
d1 = √a2 + c2 - 2ac cos α
d1 = √b2 + c2 - 2bc cos β
3. Формула довжини діагоналі через висоту та середню лінію:
d1 = √h2 + m2
4. Формула довжини діагоналі через висоту та основи:
| d1 = | 1 | √4h2 + (a + b)2 |
| 2 |
Площа рівнобічної трапеції
Формули площі рівнобічної трапеції:
1. Формула площі через сторони:
| S = | a + b | √4c2 - (a - b)2 |
| 4 |
2. Формула площі через сторони та кут:
S = (b + c cos α) c sin α = (a - c cos α) c sin α
3. Формула площі через радіус вписаного кола та кут між основою та боковою стороною:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площі через основи та кут між основою та боковою стороною:
| S = | ab | = | ab |
| sin α | sin β |
5. Формула площі рівнобічної трапеції, в яку можна вписати коло:
S = (a + b) · r = √ab·c = √ab·m
6. Формула площі через діагоналі та кут між ними:
| S = | d12 | · sin γ | = | d12 | · sin δ |
| 2 | 2 |
7. Формула площі через середню лінію, бокову сторону та кут при основі:
S = mc sin α = mc sin β
8. Формула площі через основи та висоту:
| S = | a + b | · h |
| 2 |
Коло описане навколо трапеції
Коло можна описати лише навколо рівнобічної трапеції!!!
Формула радіуса описаного навколо трапеції кола:
1. Формула радіуса через сторони та діагональ:
де
a - більша основа
| R = | a·c·d1 |
| 4√p(p - a)(p - c)(p - d1) |
| p = | a + c + d1 |
| 2 |
Формули з геометрії
Трикутник. Формули та властивості трикутника  Квадрат. Формули та властивості квадрату
Квадрат. Формули та властивості квадрату  Прямокутник. Формули та властивості прямокутника
Прямокутник. Формули та властивості прямокутника  Паралелограм. Формули та властивості паралелограма
Паралелограм. Формули та властивості паралелограма  Ромб. Формули та властивості ромба
Ромб. Формули та властивості ромба  Трапеція. Формули та властивості трапеції
Трапеція. Формули та властивості трапеції  - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції
- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції  - Прямокутна трапеція. Формули та властивості прямокутної трапеції
- Прямокутна трапеція. Формули та властивості прямокутної трапеції  Правильний многокутник. Формули і властивості правильного многокутника
Правильний многокутник. Формули і властивості правильного многокутника  Коло, круг, сегмент, сектор. Формули та властивості
Коло, круг, сегмент, сектор. Формули та властивості  Еліпс. Формули та властивості еліпса
Еліпс. Формули та властивості еліпса  Куб. Формули та властивості куба
Куб. Формули та властивості куба  Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості
Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості  Піраміда. Формули та властивості піраміди
Піраміда. Формули та властивості піраміди  Сфера, куля, сегмент та сектор. Формули та властивості
Сфера, куля, сегмент та сектор. Формули та властивості  Циліндр. Формули та властивості циліндра
Циліндр. Формули та властивості циліндра  Конус. Формули та властивості конуса
Конус. Формули та властивості конуса  Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
 Квадрат. Формули та властивості квадрату
Квадрат. Формули та властивості квадрату  Прямокутник. Формули та властивості прямокутника
Прямокутник. Формули та властивості прямокутника  Паралелограм. Формули та властивості паралелограма
Паралелограм. Формули та властивості паралелограма  Ромб. Формули та властивості ромба
Ромб. Формули та властивості ромба  Трапеція. Формули та властивості трапеції
Трапеція. Формули та властивості трапеції  - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції
- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції  - Прямокутна трапеція. Формули та властивості прямокутної трапеції
- Прямокутна трапеція. Формули та властивості прямокутної трапеції  Правильний многокутник. Формули і властивості правильного многокутника
Правильний многокутник. Формули і властивості правильного многокутника  Коло, круг, сегмент, сектор. Формули та властивості
Коло, круг, сегмент, сектор. Формули та властивості  Еліпс. Формули та властивості еліпса
Еліпс. Формули та властивості еліпса  Куб. Формули та властивості куба
Куб. Формули та властивості куба  Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості
Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості  Піраміда. Формули та властивості піраміди
Піраміда. Формули та властивості піраміди  Сфера, куля, сегмент та сектор. Формули та властивості
Сфера, куля, сегмент та сектор. Формули та властивості  Циліндр. Формули та властивості циліндра
Циліндр. Формули та властивості циліндра  Конус. Формули та властивості конуса
Конус. Формули та властивості конуса  Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
