OnlineMSchool
Вивчення математики онлайн.
Вивчайте математику з нами і переконайтесь: "Математика - це просто!"
Реєстрація Увійти Вийти

Конус. Формули, ознаки та властивості конуса

Навігація по сторінці: Визначення конуса Елементи конуса Об'єм конуса Площа поверхні конуса Рівняння конуса Основні властивості кругового конуса
Означення.
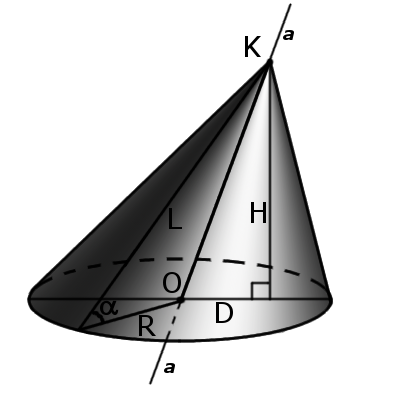
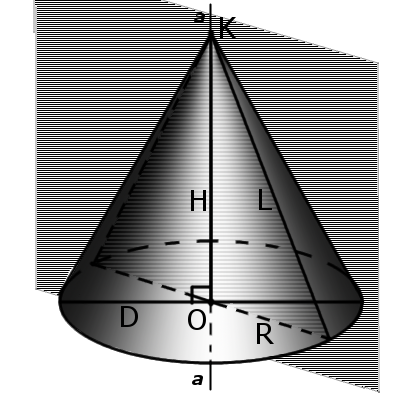
Конус — це геометричне тіло, яке утворене сукупністю всіх променів, що виходять з точки та перетинають будь-яку плоску поверхню. В місці перетину утворюється основа конуса.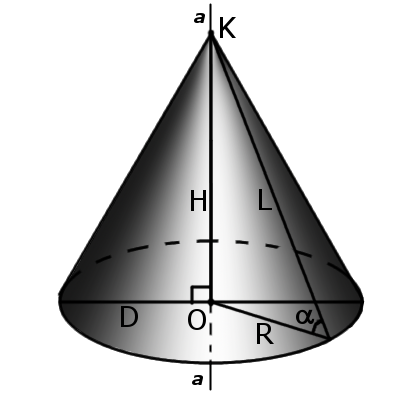
Зображення конуса з позначеннями Зображення конуса з позначеннями
Мал.1 Мал.2
 
 
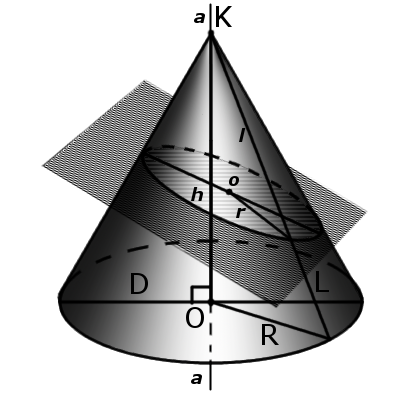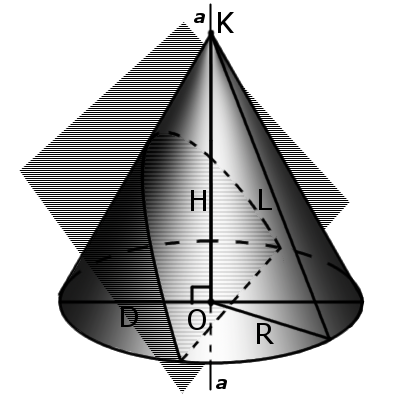Зображення конуса з позначеннями Зображення конуса з позначеннями
Мал.3 Мал.4

Елементи конуса

Означення. Вершина конуса - це точка (K), з якої виходять промені.
Означення. Основа конуса - це площина, що утворена внаслідок перетину плоскої поверхні та всіх променів, що виходять з вершини конуса. У конуса можуть бути такі основи, як круг, еліпс, гіпербола та парабола.
Означення. Твірною конуса (L) називається будь-який відрізок, які сполучає вершину конуса з межею основи конуса. Твірна є відрізком променя, що виходить з вершини конуса.
Формула. Довжина твірної (L) прямого кругового конуса через радіус R та висоту H (через теорему Піфагора):

L2 = R2 + H2

Означення. Напрямна конуса - це крива, яка описує контур основи конуса.
Означення. Бічна поверхня конуса - це сукупність усіх твірних конуса. Тобто, поверхня, яка утворюється рухом твірної по напрямній конуса.
Означення. Поверхня конуса складається з бічної поверхні та основи конуса.
Означення.Висота конуса (H) - це відрізок, який виходить з вершини конуса та перпендикулярний до його основи.
Означення. Вісь конуса (a) - це пряма, яка проходить через вершину конуса та центр основи конуса.
Означення. Конусність (С) конуса - це відношення діаметра основи конуса до його висоти. У випадку зрізаного конуса - це відношення різниці діамерів поперечних перерізів D та d зрізаного конуса до відстані між ними:
C = D      та      C = D - d
Hh
де C - конусність, D - діаметр основи, d - діаметр меншої основи та h - відстань між основами.

Конусність характеризує гостроту конуса, тобто, кут нахилу твірної до основи конуса. Чим більша конусність, тим гостріший кут нахилу. Кут конуса α буде:
α = 2arctgR
H
де R - радіус основи, а H - висота конуса.
Осьовий переріз конуса з позначеннями
Означення. Осьовий переріз конуса - це переріз конуса площиною, яка проходить через вісь конуса. Такий переріз утворює рівнобедрений трикутник, у якого сторони утворені твірними, а основа трикутника - це діаметр основи конуса.
Осьовий переріз конуса з позначеннями
Означення. Дотична площина до конуса - це площина, яка проходить через твірну конуса і перепендикулярна до осьового перерізу конуса.
Означення. Конус, що спирається на круг, еліпс, гіперболу чи параболу називається відповідно круговим, еліптичним, гіперболічним чи параболічним конусом (останні два мають нескінченний об'єм).
Прямий конус з позначеннями
Означення. Прямий конус - це конус у якого вісь перпендикулярна основі. В такого конуса вісь співпадає з висотою, а всі твірні рівні між собою.
Формула. Об'єм кругового конуса:
V = 1πHR2
3
де R - радіус основи, а H - висота конуса.
Формула. Площа бічної поверхні (Sb) прямого конуса через радіус R та довжину твірної L:

Sb = πRL

Формула. Загальна площа поверхні (Sp) прямого кругового конуса через радіус R та довжину твірної L:

Sp = πRL + πR2

Косий (похилий) конус з позначеннями
Означення. Косий (похилий) конус - це конус у якого вісь не перпендикулярна основі. В такого конуса вісь не співпадає з висотою.
Формула. Об'єм будь-якого конуса:
V = 1SH
3
де S - площа основи, а H - висота конуса.
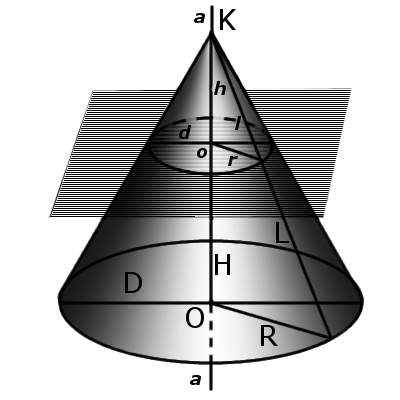
Зрізаний конус з позначеннями
Означення. Зрізаний конус - це частина конуса, яка знаходиться між основою конуса та площиною перетину, що паралельна основі.
Формула. Об'єм зрізаного конуса:
V = 1(S2H - S1h)
3
де S1 та S2 - площі меншої та більшої основи відповідно, а H та h - відстань від вершини конуса до центру нижньої та верхньої основи відповідно.

Рівняння конуса

1. Рівняння прямого кругового конуса в декартовій системі координат з координатами (x, y, z):
x2 + y2 - z2 = 0
a2a2c2
2. Рівняння прямого еліптичного конуса в декартовій системі координат з координатами (x, y, z):
x2 + y2 = z2
a2b2c2

Основні властивості кругового конуса

1. Всі твірні прямого кругового конуса рівні між собою.
2. При обертанні прямокутного трикутника навколо свого катета на 360° утворюється прямий коловий конус.
3. При обертанні рівнобедреного трикутника навколо своєї вісі на 180° утворюється прямий коловий конус.
4. В місці перетину конуса площиною, яка паралельна основі конуса, утворюється коло. (див. Зрізаний конус)
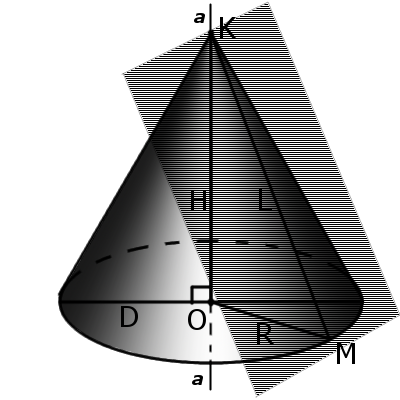
5. Якщо при перетині площина не паралельна основі конуса і не перетинається з основою, то в місці перетину утвориться еліпс (мал. 3).
6. Якщо площина перерізу проходить через основу, то в місці перетину утвориться парабола (мал. 4).
7. Якщо площина перерізу проходить через вершину, то в місці перетину утвориться рівнобедрений трикутник (див. Осьовий переріз).
8. Центр ваги будь-якого конуса знаходиться на одній четвертій висоти від центра основи.

Формули з геометрії Трикутник. Формули та властивості трикутника Квадрат. Формули та властивості квадрату Прямокутник. Формули та властивості прямокутника Паралелограм. Формули та властивості паралелограма Ромб. Формули та властивості ромба Трапеція. Формули та властивості трапеції - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції - Прямокутна трапеція. Формули та властивості прямокутної трапеції Правильний многокутник. Формули і властивості правильного многокутника Коло, круг, сегмент, сектор. Формули та властивості Еліпс. Формули та властивості еліпса Куб. Формули та властивості куба Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду Призма. Формули, ознаки та властивості Піраміда. Формули та властивості піраміди Сфера, куля, сегмент та сектор. Формули та властивості Циліндр. Формули та властивості циліндра Конус. Формули та властивості конуса Формули площі геометричних фігур S Формули периметра геометричних фігур P Формули об'єму геометричних фігур V Формули площі поверхні геометричних фігур S
Всі таблиці і формули

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!

0
Приєднуйтесь до нас