Куб. Формули, ознаки та властивості куба

Навігація по сторінці: Визначення куба Грань куба Ребро куба Вершина куба Центр грані куба Центр куба Вісь куба Діагональ куба Діагональ грані куба Об'єм куба Площа поверхні куба Периметр куба Сфера вписана в куб Сфера описана навколо куба Властивості куба Координати вершин куба Одиничний куб Перетин одиничного куба площиною

Означення.

Куб (гексаедр) — це тривимірна фігура, яка складається з шести днакових квадратів так, що кожен квадрат повністю дотикається своїми чотирма сторонами до сторін інших чотирьох квадратів під прямим кутом. Куб є правильним багатогранником у якого грані утворені з квадратів. Також кубом можна назвати прямокутний паралелепіпед, у якого всі ребра рівні.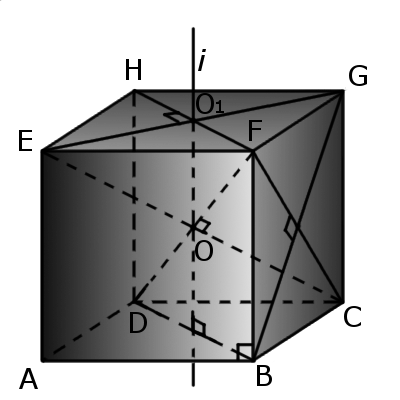

Означення. Грань куба - це частина площини, обмежена сторонами квадрату.

- куб має шість граней;

- кожна грань куба перетинається з чотирма іншими гранями під прямим кутом та паралельна шостій грані;

- грані мають однакову площу, яку можна знайт искориставшись формулами для площі квадрата.

Означення. Ребро куба - це відрізок, утворений перетином двох граней куба.

- куб має дванадцять ребер;

- кожен кінець ребра з'єднаний з кінцями двох сусідніх ребер під прямим кутом;

- ребра куба мають однакову довжину.

Означення. Вершина куба - це найвіддаленіша точка від центру куба, яка лежить на перетині трьох граней куба.

- куб має вісім вершин;

- кожна вершина утворена тільки трьома гранями та трьома ребрами.

Означення. Центр грані куба (O₁) - це рівновіддалена точка від усіх ребер грані куба.

Означення. Центр куба (O) - це рівновіддалена точка від усіх граней куба.

Означення. Вісь куба (i) - це пряма, яка проходить через центр куба та цетри двох паралельних граней куба.

- куб має три вісі;

- вісі куба взаємно перпендикулярні.

Означення. Діагональ куба (d₁) - відрізок, який з'єднує протилежні вершини куба та проходить через центр куба.

- куб має чотири діагоналі;

- діагоналі куба перетинаються під прямим кутом та діляться навпіл у центрі куба;

- діагоналі куба мають однакову довжину.

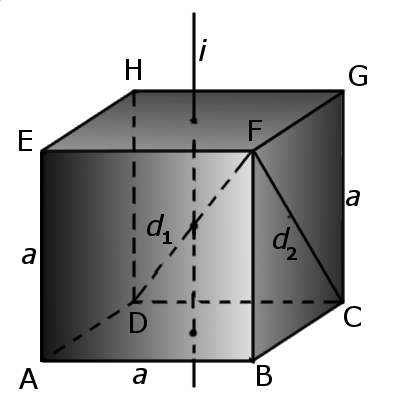
Формула. Діагональ куба d₁ через довжину ребра a:

d₁ = a√3

Означення. Діагональ грані куба (d₂) - відрізок, який з'єднує протилежні кути грані куба та проходить через центр грані куба.

Формула. Діагональ грані d₂ через довжину ребра a:

d₂ = a√2

Означення. Об'єм куба - це сукупність усіх точок в просторі, що обмежені гранями куба.

Формула. Об'єм куба через довжину ребра a:

V = a³

Формула. Об'єм куба через довжину діагоналі куба d₁:

V =	d₁³
	3√3

Означення. Площа поверхні куба - це сукупність площин усіх граней.

Формула. Площа поверхні куба через довжину ребра a:

S = 6a²

Означення. Периметр куба - це сукупність довжин всіх ребер куба.

Формула. Периметр куба P через довжину ребра a:

P = 12a

Означення. Сферою вписаною в куб називається сфера, яка має центр спільний з центром куба та дотикається до центрів граней куба.

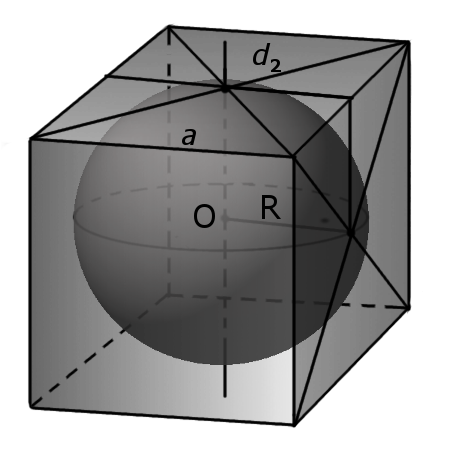
- всі шість граней куба є дотичними площинами до вписаної сфери;

- радіус вписаної сфери дорівнює половині довжини ребра a.

Формула. Радіус вписаної сфери r через довжину ребра a:

r =	a
	2

Формула. Об'єму вписаної сфери V через довжину ребра a:

V =	π a³
	6

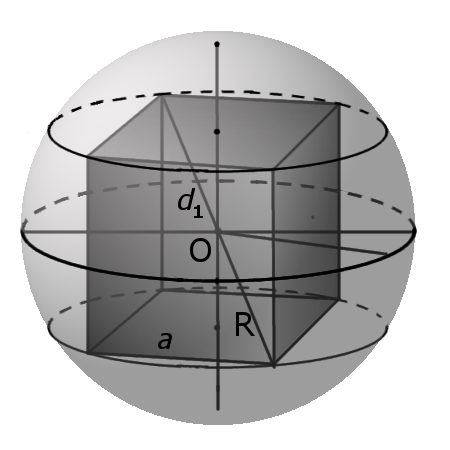
Сфера описана навколо куба з позначеннями

Означення. Сферою описаною навколо куба називається сфера, яка має центр спільний з центром куба та дотикається до восьми вершин куба.

- радіус описаної сфери рівний половині довжини діагоналі (d₁) куба.

Формула. Радіус описаної сфери R через довжину ребра a:

R =	a√3
	2

Формула. Об'єму сфери описаної навколо куба V через довжину ребра a:

V =	π a³√3
	2

Властивості куба

1. В куб можна вписати тетраедр так, щоб всі чотири вершини тетраедра лежали на чотирьох вершинах куба, а всі шість ребер тетраедра лежатимуть на шести гранях куба і ребра будуть рівні діагоналі грані куба.

2. Куб описує октаедр так, що всі шість вершин октаедра лежать в центрах граней куба.

3. Октаедр описує куб так, щоб всі вісім вершин куба розташовані в центрах восьми граней октаедра.

Координати вершин куба

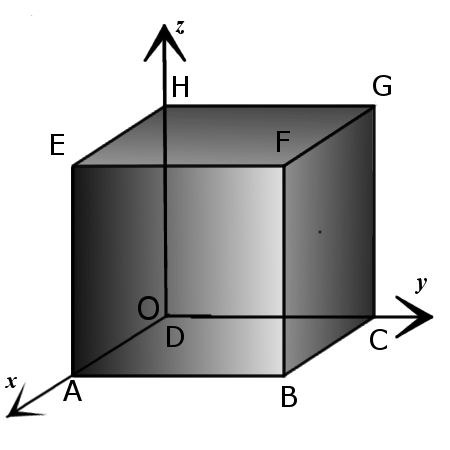
1. Координати вершин куба зі стороною a та вершиною D у початку декартової системи координат так, що ребра цієї вершини лежать на вісях координат:

A(a, 0, 0), B(a, a, 0), C(0, a, 0), D(0, 0, 0),
E(a, 0, a), F(a, a, a), G(0, a, a), H(0, 0, a).

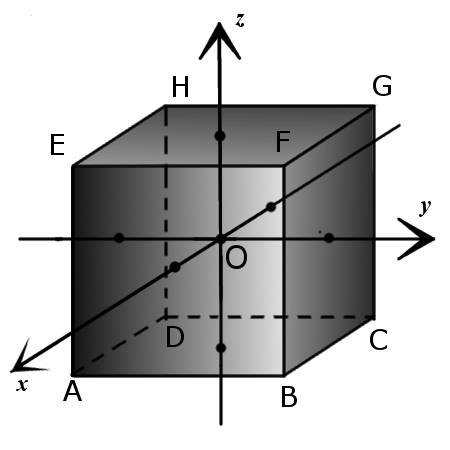
2. Координати вершин куба з довжиною сторони 2a, у якого центр куба розташований в початку декартової системи координат так, що ребра куба паралельні вісям координат:

A(a, -a, -a), B(a, a, -a), C(-a, a, -a), D(-a, -a, -a),
E(a, -a, a), F(a, a, a), G(-a, a, a), H(-a, -a, a).

Означення. Одиничний куб - це куб, у якого довжина ребер дорівнює одиниці.

Перетин куба площиною

1. Якщо перетнути куб площиною, яка проходить через центр куба та центри двох протилежних граней, то в перерізі буде квадрат довжина сторони, якого буде дорівнювати довжені ребра куба. Ця площина ділить куб два рівних прямокутних паралелепіпеда.

2. Якщо перетнути куб з ребром a площиною, яка проходить через центр куба та два паралельних ребра, то в перерізі буде прямокутник зі сторонами a і a√2, площею перерізу a²√2. Ця площина ділить куб дві рівні призми.

3. Якщо перетнути куб площиною, яка проходить через центр та середини шести граней, то в перерізі буде правильний шестикутник зі стороною a√2/2, площею перерізу a²(3√3)/4. У куба одна з діагоналей (FC) кожної грані, що перерізаються, перпендикулярна до сторони шестикутника.

4. Якщо перетнути куб площиною, яка проходить через три вершини куба, то в перерізі буде правильний трикутник зі стороною a√2, площею перерізу a²√3/2 та об'ємом більшої частини - 5a³/6 та меншої - a³/6. Одна з діагоналей куба (EC) перпендикулярна до площини перерізу та проходить через центр трикутника (M) та ділиться площиною в выдношенні MC:EМ = 2:1.

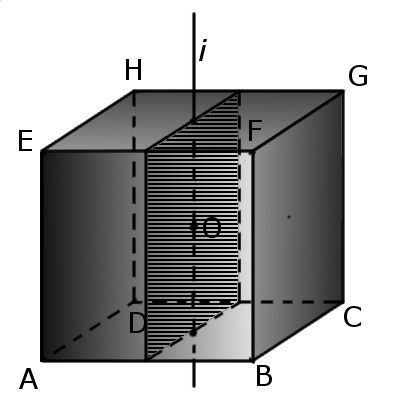
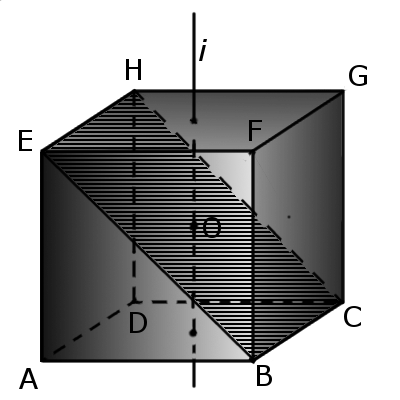
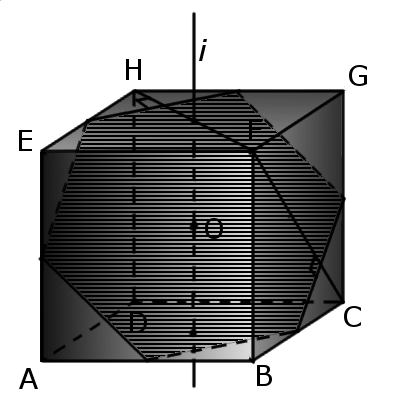
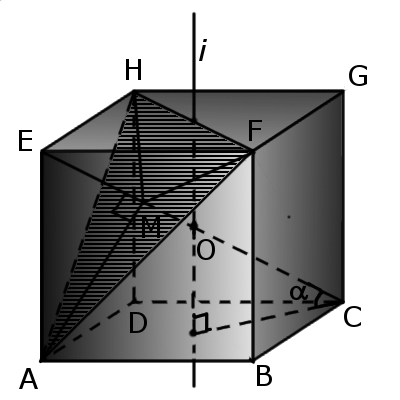
Формули з геометрії Трикутник. Формули та властивості трикутника