Перетин прямих. Точка перетину двох прямих
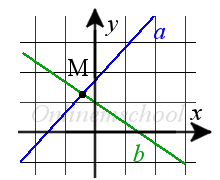
Якщо точка M є точкою перетину двох прямих, то вона повинна належати цим прямим, а її координати задовольняти рівняння цих прямих.
Точка перетину двох прямих на площині
- графічний
- аналітичний
Якщо система рівнянь:
- має єдине розв'язок, то прямі перетинаються;
- має нескінченну кількість розв'язків, то прямі співпадають;
- не має розв'язків, то прямі не перетинаються (прямі паралельні між собою)
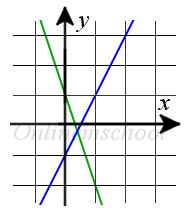
Розв'язок: Для обчислення координат точки перетину прямих, розв'яжемо систему рівнянь:
Віднімемо з першого рівняння друге
З першого рівняння знайдемо значення x
Підставимо значення x у друге рівняння та знайдемо значення y
Відповідь. Точка перетину двох прямих має координати (0.4, -0.2)
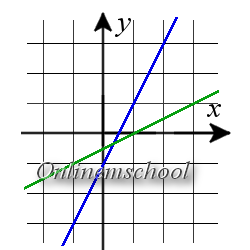
Розв'язок: Для обчислення координат точки перетину прямих, розв'яжемо систему рівнянь:
У перше рівняння підставимо значення x та y з другого та третього рівнянь.
Підставимо значення t у друге та третє рівняння
Відповідь. Точка перетину двох прямих має координати (
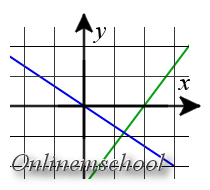
Розв'язок: Для обчислення координат точки перетину прямих, розв'яжемо систему рівнянь:
З другого рівняння виразимо y через x
Підставимо y у перше рівняння
Відповідь. Точка перетину двох прямих має координати (
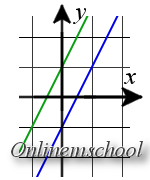
Розв'язок: Обидві прямі задані рівняннями із кутовим коефіцієнтом. Так як k1 = k2 = 2, то прямі паралельні. Так як ці прямі не збігаються точок перетину немає.
Вирішимо також це завдання використовуючи систему рівнянь:
Віднімемо з першого рівняння друге
У першому рівнянні отримали протиріччя (0 ≠ -2), отже система не має рішень - відсутні точки перетину прямих (прямі паралельні).
Відповідь. Прямі не перетинаються (прямі паралельні).
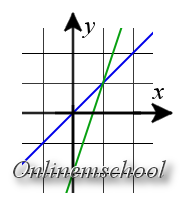
Розв'язок: Підставимо координати точки N у рівняння прямих.
1 = 1
1 = 3·1 - 2 = 1
Відповідь. Так як обидва рівняння перетворилися на тотожність, то точка N - точка перетину цих прямих.
Точка перетину двох прямих у просторі
Якщо система рівнянь:
- має єдине рішення, що прямі перетинаються;
- має безліч рішень, то прямі співпадають;
- немає рішень, то прямі не перетинаються
Розв'язок: Складемо систему рівнянь
Підставимо значення x, y, z з 1, 2, 3 рівнянь в 4, 5, 6 рівняння
До шостого рівняння додамо п'яте рівняння
Підставимо значення b у четверте та п'яте рівняння
Відповідь. Прямі перетинаються у точці з координатами (1, 1, 1).
Розв'язок: Складемо систему рівнянь замінивши у другому рівнянні параметр t на a
Підставимо значення x, y, z з 1, 2, 3 рівнянь у 4, 5, 6 рівняння
Підставимо значення t з шостого рівняння до інших рівнянь
Відповідь. Так як -6 ≠
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
