Кут між прямою та площиною
Формула для обчислення кута між прямою та площиною
Якщо в просторі задані напрямний вектор прямої L
s = {l; m; n}
і рівняння площини
Ax + By + Cz + D = 0,
то кут між цією прямою і площиною можна знайти використав формулу
| sin φ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
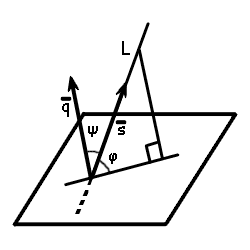
Виведення формули обчислення кута між прямою та площиною
З рівняння прямої можна знайти напрямний вектор прямої
s = {l; m; n}З рівняння площини вектор нормалі площини має вигляд
q = {A; B; C}З формул скалярного добутку векторів знайдемо косинус кута між нормаллю до площини та напрямним вектором прямої
| cos ψ = | | q · s | |
| | s | · |q | |
Так як φ = 90° - ψ, то синус кута між прямою і площиною sin φ = cos ψ.
Розписавши скалярний добуток векторів і модулі векторів через їх координати, отримаємо формулу для обрахунку кута між прямою та площиною.
Приклад обрахунку кута між прямою та площиною
Приклад 1. Знайти кут між прямою
x - 4
=
y + 2
= -
z - 6
2
6
3
та площиною x - 2y + 3z + 4 = 0.
Розв'язок.
З рівняння прямої знайдемо напрямний вектор прямої
s = {2; 6; -3}
З рівняння площини знайдемо вектор нормалі площини
q = {1; -2; 3}
Скориставшись формулою, знайдемо кут між прямою та площиною
sin φ =
| 2 · 1 + 6 · (-2) + (-3) · 3 |
=
√22 + 62 + (-3)2 · √12 + (-2)2 + 32
sin φ =
| 2 - 12 - 9 |
=
19
=
19
√4 + 36 + 9 · √1 + 4 + 9
√49 · √14
7√14
Відповідь:
sin φ =
19
7√14
| x - 4 | = | y + 2 | = - | z - 6 |
| 2 | 6 | 3 |
Розв'язок.
З рівняння прямої знайдемо напрямний вектор прямої
s = {2; 6; -3}З рівняння площини знайдемо вектор нормалі площини
q = {1; -2; 3}Скориставшись формулою, знайдемо кут між прямою та площиною
| sin φ = | | 2 · 1 + 6 · (-2) + (-3) · 3 | | = |
| √22 + 62 + (-3)2 · √12 + (-2)2 + 32 |
| sin φ = | | 2 - 12 - 9 | | = | 19 | = | 19 |
| √4 + 36 + 9 · √1 + 4 + 9 | √49 · √14 | 7√14 |
| Відповідь: |
|
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
