Відстань від точки до площини
Навігація по сторінці:
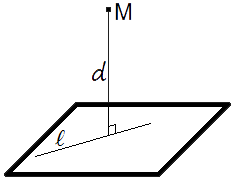
Означення.
Відстань від точки до площини — дорівнює довжині перпендикуляра, опущеного з точки на площину.Формула для обчислення відстані від точки до площини
Якщо задано рівняння площини Ax + By + Cz + D = 0, то відстань від точки M(Mx, My, Mz) до площини можна знайти використовуючи наступну формулу:
| d = | |A·Mx + B·My + C·Mz + D| |
| √A2 + B2 + C2 |
Приклади задач на обчислення відстані від точки до площини
Приклад 1.
Знайти відстань між площиною 2x + 4y - 4z - 6 = 0 і точкою M(0, 3, 6).
Розв'язок. Підставимо в формулу коефіцієнти прямої і координати точки
| d = | |2·0 + 4·3 + (-4)·6 - 6| | = | |0 + 12 - 24 - 6| | = | |- 18| | = 3 |
| √4 + 16 + 16 | √36 | 6 |
Відповідь: відстань від точки до площини дорівнює 3.
Аналітична геометрія: Вступ та змістВідстань між двома точкамиСередина відрізку. Координати середини відрізкуРівняння прямоїТочка перетину прямихКут міжд прямимиРівняння площиниВідстань від точки до площиниВідстань між площинамиВідстань від точки до прямої на площиніВідстань від точки до прямої в просторіКут між площинамиКут між прямою та площиною
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
