Кут між прямими

Навігація по сторінці:

Означення кута між прямими
Кут між прямими на площині
Приклади завдань для обчислення кута між прямими на площині
Кут між прямими в просторі

Онлайн калькулятор для обчислення кута між прямими

Означення кута між прямими

Дві прямі називаються такими, що перетинаються, якщо вони мають єдину спільну точку. Ця точка називається точкою перетину прямих. Прямі розбиваються точкою перетину на промені, які утворюють чотири нерозгорнуті кути, серед яких дві пари вертикальних кутів і чотири пари суміжних кутів. Якщо відомий розмір одного з кутів, утворених прямими, що перетинаються, то легко визначити розмір інших кутів. Якщо один із кутів прямий, то решта теж прямі, а прямі перпендикулярні.

Означення Кут між прямими - розмір найменшого з кутів, утворених цими прямими.

Кут між прямими на площині

Кут між прямими заданими рівняннями з кутовим коефіцієнтом

Якщо дві прямі задано рівняннями з кутовим коефіцієнтом

y = k₁x + b₁,
y = k₂x + b₂,

то кут між ними можна знайти за допомогою формули:

tg γ = k₁ - k₂1 + k₁·k₂

Якщо знаменник дорівнює нулю (1 + k₁·k₂ = 0), то прямі перпендикулярні.

Доведення. Якщо прямі задані рівняннями з кутовими коефіцієнтами, легко знайти кути між цими прямими і віссю OX

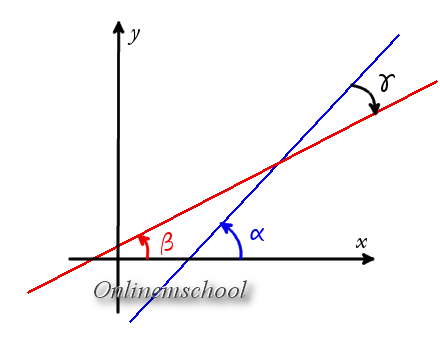
tg α = k₁
tg β = k₂

Відповідно, легко знайти кут між прямими

γ = α - β

tg γ = tg (α - β) = tg α - tg β1 + tg α ·tg β = k₁ - k₂1 + k₁·k₂

Кут між прямими через напрямні вектори цих прямих

Якщо a - напрямний вектор першої прямої та b - напрямний вектор другої прямої, то скориставшись скалярним добутком векторів, легко знайти кут між прямими:

cos φ = |a · b||a| · |b|

Якщо рівняння прямої задано параметрично

x = l t + ay = m t + b

то вектор напрямної має вигляд {l; m}

Якщо рівняння прямої задано як

A x + B y + C = 0

то для обчислення напрямного вектора можна взяти дві точки на прямій.
Нариклад, якщо C ≠ 0, A ≠ 0, C ≠ 0 , коли x = 0 => y = -CB значить точка на прямій має координати K(0, -CB), коли y = 0 => x = -CA значить точка на прямій має координати M(-CA, 0). Напрямний вектор KM = {-CA; CB}.

Якщо задане канонічне рівняння прямої

x - x₀ l = y - y₀m

то напрямний вектор має вигляд {l; m}

Якщо задане рівняння прямої з кутовим коефіцієнтом

y = kx + b

то для обчислення напрямного вектора, можна взяти дві точки на прямій, наприклад, коли x = 0 => y = b значить точка на прямій має координати K(0, b), коли x = 1 => y = k + b значить точка на прямій має координати M(1, k + b). Напрямний вектор KM = {1; k}

Кут між прямими через вектори нормалей цих прямих

Якщо a - вектор нормалі першої прямої і b - вектор нормалі другої прямої, скориставшись скалярним добутком векторів, легко знайти кут між прямими:

cos φ = |a · b||a| · |b|

Якщо рівняння прямої задане як

A x + B y + C = 0

то вектор нормалі має вигляд {A; B}

Якщо задане рівняння прямої з кутовим коефіцієнтом

y = kx + b

то вектор нормалі має вигляд {1; -k}

Кут між прямими через напрямний вектор та вектор нормалі цих прямих

Якщо a - напрямний вектор першої прямої і b - вектор нормалі другої прямої, скориставшись скалярним добутком векторів, легко знайти кут між прямими:

sin φ = |a · b||a| · |b|

Приклади завдань для обчислення кута між прямими на площині

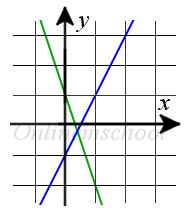
Приклад 1. Знайти кут між прямими y = 2x - 1 та y = -3x + 1.

Розв'язок: Скористаємося формулою для обчислення кута між прямими заданими рівняннями з кутовим коефіцієнтом:

tg γ = k₁ - k₂1 + k₁·k₂ = 2 - (-3)1 + 2·(-3) = 5-5 = 1

Відповідь. γ = 45°

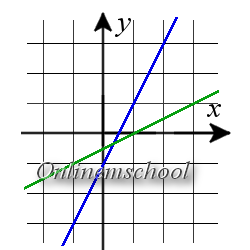
Приклад 2. Знайти кут між прямими y = 2x - 1 та x = 2t + 1y = t.

Розв'язок: Скористаємося формулою для обчислення кута між прямими, у яких відомі напрямні вектори.

Для першої прямої напрямний вектор {1; 2}, для другої прямої напрямний вектор {2; 1}

cos φ = |1 · 2 + 2 · 1|1² + 2² · 2² + 1² = 45 · 5 = 0.8

Відповідь. φ ≈ 36.87°

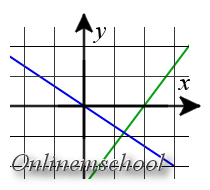
Приклад 3 Знайти кут між прямими 2x + 3y = 0 та x - 23 = y4.

Розв'язок: Для розв'язання цього завдання можна знайти напрямні вектори та обчислити кут через напрямні вектори або перетворити рівняння на рівняння з кутовим коефіцієнтом та обчислити кут через кутові коефіцієнти.

Перетворимо наявні рівняння у рівняння з кутовим коефіцієнтом.

2x + 3y = 0 => y = -23x (k₁ = -23)

x - 23 = y4 => y = 43x - 83 (k₂ = 43)

tg γ = k₁ - k₂1 + k₁·k₂ = -23 - 431 + (-23)·43 = -631 - 89 = 18

Відповідь. γ ≈ 86.82°

Кут між прямими у просторі

Якщо a - напрямний вектор першої прямої, а b - напрямний вектор другої прямої, скориставшись скалярним добутком векторів, легко знайти кут між прямими:

cos φ = |a · b||a| · |b|

Якщо дано канонічне рівняння прямих

x - x₀ l = y - y₀m = z - z₀n

то напрямний вектор має вигляд {l; m; n}

Якщо рівняння прямої задане параметрично

x = l t + ay = m t + bz = n t + c

то напрямний вектор має вигляд {l; m; n}

Приклад 4. Знайти кут між прямими x = 2t + 1y = tz = -t - 1 та x = t + 2y = -2t + 1z = 1.

Розв'язок: Оскільки прямі задані параметрично, то {2; 1; -1} - напрямний вектор першої прямої, {1; -2; 0} - напрямний вектор другої прямої.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0|2² + 1² + (-1)² · 1² + (-2)² + 0² = 06 · 5 = 0

Відповідь. φ = 90°

Приклад 5 Знайти кут між прямими x - 23 = y4 = z - 35 та -x - 22 = 1 - 3y = 3z - 52.

Розв'язок: Щоб вирішити це завдання, знайдемо напрямні вектори цих прямих.

Рівняння першої прямої задано в канонічному виді, тому напрямний вектор {3; 4; 5}.

Перетворимо друге рівняння до канонічного вигляду.

-x - 22 = x - 2-2

1 - 3y = 1 + y-1/3 = y - 1/3-1/3

3z - 52 = z - 5/32/3

Отримано рівняння другої прямої у канонічному вигляді

x - 2-2 = y - 1/3-1/3 = z - 5/32/3

{-2; -13; 23} - напрямний вектор другої прямої.

cos φ = 3·(-2) + 4·(-13) + 5·233² + 4² + 5² · (-2)² + (-13)² + (23)² = -6 - 43 + 1039 + 16 + 25 · 4 + 19 + 49 = -450 · 41/9 = 12582 = 682205

Відповідь. φ ≈ 74.63°

Аналітична геометрія: Вступ та зміст Відстань між двома точками Середина відрізку. Координати середини відрізку Рівняння прямої Точка перетину прямих Кут міжд прямими Рівняння площини Відстань від точки до площини Відстань між площинами Відстань від точки до прямої на площині Відстань від точки до прямої в просторі Кут між площинами Кут між прямою та площиною

Онлайн калькулятори. Аналітична геометрія. Декартові координати.

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!