Десятковий логарифм

Навігація по сторінці:

Означення
Калькулятор
Властивості
Приклади

Означення. Логарифмом числа b за основою a, де a > 0, a ≠ 1, b > 0, називається показник степеню, до якого потрібно підвести основу a, щоб отримати число b.

Означення. Десятковий логарифм — логарифм за основою 10.

Іншими словами, десятковий логарифм числа b є розв'язком рівняння 10^x = b.

Позначення. Десятковий логарифм позначається lg x або log₁₀ x.

Калькулятор десяткових логарифмів

lg 2

Властивості десяткових логарифмів

Для будь яких x > 0 и y > 0 виконуються наступні властивості десяткових логарифмів.

lg x = log₁₀ x - так як основа десяткового логарифма рівна 10.
10^{lg b} = b.
lg 1 = 0
lg 10 = 1
lg 10ⁿ = n
lg(x · y) = lg x + lg y
lg xy = lg x - lg y
lg xⁿ = n lg x
Графік функції y = lg x
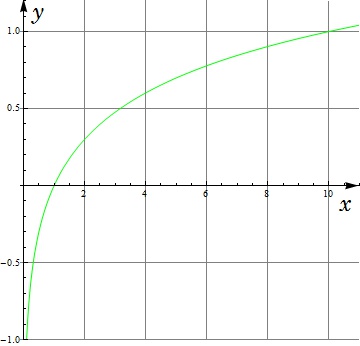
(lg x)′ = 1x ln 10
∫ lg x dx = x lg x - xln 10 + C
lim lg x = -∞

x → +0

Приклад 1. Знайти значення десяткового логарифму від чисел 100, 1000, 0.1, 0.01, 0.001.

lg 100 = lg 10² = 2

lg 1000 = lg 10³ = 3

lg 0.1 = lg 10^-1 = -1

lg 0.01 = lg 10^-2 = -2

lg 0.001 = lg 10^-3 = -3

Приклад 2.

Довести рівність: a ^{lg b} = b ^{lg a}.

Запишемо очевидну рівність:

lg b · lg a = lg a · lg ab

Піднесемо 10 до відповідного степеню

10^{lg b · lg a} = 10^{lg a · lg b}

(10^{lg b})^{lg a} = (10^{lg a})^{lg b}

b^{lg a} = a^{lg b}

Рівність доведено.

Приклад 3.

Знаючи, що lg 2 = a, lg 3 = b, lg 5 = c, виразити lg 6; lg 30; lg 16 через a, b, c.

Використавши формули логарифму добутку та степеню отримаємо:

lg 6 = lg (2·3)= lg 2 + lg 3 = a + b;

lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c;

lg 16 = lg 2⁴= 4 · lg 2 = 4a.

Приклад 4.

Обчислити log₉ 5 · log₂₅ 27.

Перейдемо до основи 10:

log₉ 5 · log₂₅ 27 = lg 5lg 9 · lg 27lg 25

Використаємо властивість логарифму степеню lg xⁿ = n lg x:

lg 5lg 9 · lg 27lg 25 = lg 5lg 3² · lg 3³lg 5² = lg 52 lg 3 · 3 lg 32 lg 5 = 34

Приклад 5.

Обчислити log₃₀ 8, якщо lg 5 = a, lg 3 = b.

Перейдемо до основи 10:

log ₃₀ 8 = lg 8lg 30 = lg 2³lg (3 · 10) =

Використаємо властивості логарифму добутку, частки та те що 2= 105:

= 3 lg 2lg 3 + lg 10 = 3 lg 2lg 3 + 1 = 3 lg 105lg 3 + 1 = 3(lg 10 - lg 5)lg 3 + 1 = 3(1 - lg 5)lg 3 + 1 =

Підставимо lg 5 = a, lg 3 = b:

= 3(1 - a)b + 1

Відповідь:

log₃₀ 8 = 3(1 - a)b + 1

Логарифми Логарифм числа, основна логарифмічна тотожність Формули і властивості логарифмів Логарифм добутку. Сума логарифмів Логарифм частки. Різниця логарифмів Логарифм степені Логарифм кореня Логарифмування Потенціювання Десятковий логарифм Натуральний логарифм Число е Логарифмічна функція Логарифмічні рівняння Логарифмічні нерівності

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!

lim	lg x = -∞
x → +0