Логарифмічні нерівності

Означення. Логарифмічні нерівності - це нерівності, що містять змінну під знаком логарифма.

Наприклад: log₃ (x² - 3 x + 3) > 1.

При розв'язанні логарифмічних нерівностей пам'ятаємо:

загальні властивості нерівностей;
властивість монотонності логарифмічної функції;
область визначення логарифмічної функції.

Основні методи розв'язування логарифмічних нерівностей

log_a f(x) > b a > 1 <=> f(x) > a^b
log_a f(x) > b 0 < a < 1 <=> 0 < f(x) < a^b
log_a f(x) < b a > 1 <=> 0 < f(x) < a^b
log_a f(x) < b 0 < a < 1 <=> f(x) > a^b
log_g(x) f(x) > b <=> f(x) > g(x)^b g(x) > 1 f(x) < g(x)^b 0 < g(x) < 1 f(x) > 0
log_g(x) f(x) < b <=> f(x) < g(x)^b g(x) > 1 f(x) > 0 f(x) > g(x)^b 0 < g(x) < 1
log_a f(x) > log_a h(x) a > 1 <=> f(x) > h(x) h(x) > 0
log_a f(x) > log_a h(x) 0 < a < 1 <=> f(x) < h(x) f(x) > 0
log_a f(x) < log_a h(x) a > 1 <=> f(x) < h(x) f(x) > 0
log_a f(x) < log_a h(x) 0 < a < 1 <=> f(x) > h(x) h(x) > 0
log_g(x) f(x) > log_g(x) h(x) <=> f(x) > h(x) g(x) > 1 h(x) > 0 f(x) < h(x) 0 < g(x) < 1 f(x) > 0
log_g(x) f(x) < log_g(x) h(x) <=> f(x) < h(x) g(x) > 1 f(x) > 0 f(x) > h(x) 0 < g(x) < 1 h(x) > 0

Приклади розв'язання логарифмічних нерівностей

Приклад 1.

Розв'язати нерівність log₂ (x² + 3x) ≤ 2.

Так як основа логарифму 2 > 1, то скористаємось третім методом для розв'язання нерівностей

log₂ (x² + 3x) ≤ 2 => 0 < x² + 3x ≤ 2² => x² + 3x ≤ 4 x² + 3x > 0 => x² + 3x -4 ≤ 0 x(x + 3) > 0 => (x + 4)(x -1) ≤ 0 x(x + 3) > 0

Знайдемо спільний розв'язок:

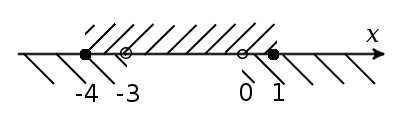
x ∈ [-4; -3) ∪ (0; 1]

Відповідь: x ∈ [-4; -3) ∪ (0; 1].

Приклад 2.

Розв'язати нерівність log_{x - 3} (x - 1) < 2.

Використаємо другу схему для розв'язання нерівності

log_{x - 3} (x - 1) < 2 => x - 1 < (x - 3)² x - 3 > 1 x - 1 > 0 x - 1 > (x - 3)² 0 < x - 3 < 1 => x - 1 < x² - 6x + 9 x > 4 x > 1 x - 1 > x² - 6x + 9 3 < x < 4 => x² - 7x + 10 > 0 x > 4 x² - 7x + 10 < 0 3 < x < 4 => (x - 2)(x -5) > 0 x > 4 (x - 2)(x -5) < 0 3 < x < 4 => x ∈ (-∞; 2) ∪ (5; +∞) x > 4 x ∈ (2; 5) 3 < x < 4 => x ∈ (5; +∞) x ∈ (3; 4) => x ∈ (3; 4) ∪ (5; +∞)

Відповідь: x ∈ (3; 4) ∪ (5; +∞).

Приклад 3.

Розв'язати нерівність log²_0.5 x + log_0.5 x - 2 ≤ 0.

ОДЗ x > 0.

Зробимо заміну log_0.5 x = t

t² + t - 2 ≤ 0

(t + 2)(t - 1) ≤ 0

-2 ≤ t ≤ 1

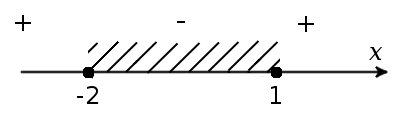
Повернемся до змінної x і з врахуванням ОДЗ розв'яжемо нерівність:

t ≥ -2 t ≤ 1 => log_0.5 x ≥ -2 log_0.5 x ≤ 1 =>

Так як основа логарифму 0.5 < 1

=> x ≤ 0.5^-2 x ≥ 0.5¹ => x ≤ 4 x ≥ 0.5

Відповідь: x ∈ [0.5; 4].

Приклад 4.

Розв'язати нерівність: log_0.4 x + log_0.4 (x - 1) ≥ log_0.4 (x + 3).

ОДЗ: x > 0 x - 1 > 0 x + 3 > 0 => x > 0 x > 1 x > -3 => x > 1

Скориставшись властивістю, суми логарифмів, перепишемо нерівність:

log_0.4 x(x - 1) ≥ log_0.4 (x + 3)

Так як основа логарифму 0.4 < 1 використаємо 8 схему для розв'язання нерівностей, з врахуванням ОДЗ:

x(x - 1) ≤ x + 3 x > 1 => x² - x ≤ x + 3 x > 1 => x² - 2x - 3 ≤ 0 x > 1 => (x + 1)(x - 3) ≤ 0 x > 1

Знайдемо спільний розв'язок:

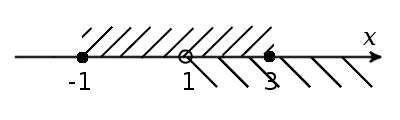
Відповідь: x ∈ (1; 3].

Приклад 5.

Розв'язати нерівність: (3 - 2x) log_0.1 x < 0.

ОДЗ: x > 0

Знайдемо нулі функції, що стоїть в лівій частині нерівності:

(3 - 2x) log_0.1 x = 0 => 3 - 2x = 0 log_0.1 x = 0 => x = 1.5 x = 1

Застосовуючи метод інтервалів, знайдемо розв'язок:

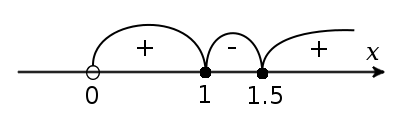
Відповідь: x ∈ (1; 1.5).

Логарифми Логарифм числа, основна логарифмічна тотожність Формули і властивості логарифмів Логарифм добутку. Сума логарифмів Логарифм частки. Різниця логарифмів Логарифм степені Логарифм кореня Логарифмування Потенціювання Десятковий логарифм Натуральний логарифм Число е Логарифмічна функція Логарифмічні рівняння Логарифмічні нерівності

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!