Відстань між двома точками
Навігація по сторінці:
Означення. Відстань між двома точками — це довжина відрізку, що з'єднує ці точки.
Формула для обчислення відстані між двома точками:
- Формула обрахунку відстані між двома точками A(xa, ya) і B(xb, yb) на площині:
AB = √(xb - xa)2 + (yb - ya)2 - Формула обрахунку відстані між двома точками A(xa, ya, za) і B(xb, yb, zb) в просторі:
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2
Виведення формули для обчислення відстані між двома точками на площині
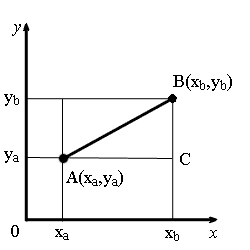
З точок A та B опустимо перпендикуляри на осі координат.
Розглянемо прямокутний трикутник ∆ABC. Катети цього трикутника дорівнюють:
BC = yb - ya.
Використавши теорему Піфагора, обрахуємо довжину відрізку AB:
Підставивши в цей вираз довжини відрізків AC та BC, виражені через координати точок A та B, отримаємо формулу для обрахунку відстані між точками на площині.
Формула для обчислення відстані між двома точками в просторі доводиться аналогічно.
Приклади задач на обчислення відстані між двома точками
Приклади обчислення відстані між двома точками на площині
Приклад 1.
Знайти відстань між точками A(-1, 3) і B(6,2).
Розв'язок.
Відповідь: AB = 5√2.
Приклади обчислення відстані між двома точками в просторі
Приклад 2.
Знайти відстань між точками A(-1, 3, 3) і B(6, 2, -2).
Розв'язок.
= √(6 - (-1))2 + (2 - 3)2 + (-2 - 3)2 = √72 + 12 + 52 = √75 = 5√3
Відповідь: AB = 5√3.
Аналітична геометрія: Вступ та змістВідстань між двома точкамиСередина відрізку. Координати середини відрізкуРівняння прямоїТочка перетину прямихКут міжд прямимиРівняння площиниВідстань від точки до площиниВідстань між площинамиВідстань від точки до прямої на площиніВідстань від точки до прямої в просторіКут між площинамиКут між прямою та площиною
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
