Відстань від точки до прямої в просторі
Формула для обчислення відстані від точки до прямої в просторі
Якщо s = {m; n; p} - напрямний вектор прямої l, M1(x1, y1, z1) - точка що належить прямій, тоді відстань від точки M0(x0, y0, z0) до прямої l можна знайти, використовуючи формулу
| d = | |M0M1×s| |
| |s| |
Виведення формули обчислення відстані від точки до прямої в просторі
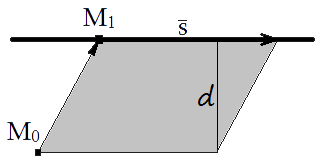
Якщо задано рівняння прямої l то нескладно знайти s = {m; n; p} - напрямний вектор прямої і M1(x1, y1, z1) - координати точки що належить цій прямій. Із властивостей векторного добутку відомо, що модуль векторного добутку векторів дорівнює площі паралелограма побудованого на цих векторах
S = |M0M1×s|.
З іншого боку площа паралелограма дорівнює добутку його сторони на висоту проведену до цієї сторони
S = |s|d.
В нашому випадку висота буде дорівнювати відстані від точки до площини d, а сторона паралелограма дорівнює модулю напрямного вектора s.
Прирівняв площі нескладно отримати формулу відстані від точки до прямої.
Приклади задач на обчислення відстані від точки до прямої в просторі
| x - 3 | = | y - 1 | = | z + 1 |
| 2 | 1 | 2 |
Розв'язок.
Із рівняння прямої отримаємо:
s = {2; 1; 2} - напрямний вектор прямої;
M1(3; 1; -1) - точка що належить прямій.
Тоді
M0M1 = {3 - 0; 1 - 2; -1 - 3} = {3; -1; -4}
| M0M1×s = | i | j | k | = |
| 3 | -1 | -4 | ||
| 2 | 1 | 2 |
= i ((-1)·2 - (-4)·1) - j (3·2 - (-4)·2) + k (3·1 -(-1)·2) = {2; -14; 5}
| d = | |M0M1×s| | = | √22 + (-14)2 + 52 | = | √225 | = | 15 | = 5 |
| |s| | √22 + 12 + 22 | √9 | 3 |
Відповідь: відстань від точки до прямої дорівнює 5.
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
