Еліпс. Формули, елементи та властивості еліпса
Навігація по сторінці:
Означення еліпса
Елементи еліпса
Основні властивості еліпса
Рівняння еліпса
Радіус кола вписаного в еліпс
Радіус кола описаного навколо еліпса
Площа еліпса
Площа сегмента еліпса
Наближена формула периметра еліпса
Довжина дуги еліпса
Означення еліпса
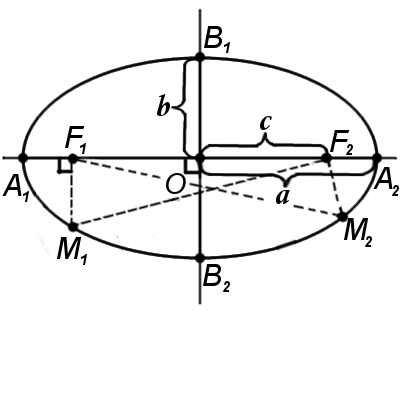
Означення. Еліпс — це замкнена плоска крива, сума відстаней від кожної точки якої до двох фіксованих точок F1 і F2 дорівнює сталій величині. Точки F1 і F2 називають фокусами еліпса.
F1M1 + F2M1 = F1M2 + F2M2 = A1A2 = const
 |
 |
|
| Рис.1 | Рис.2 |
Елементи еліпса
F1 і F2 - фокуси еліпса
Вісі еліпса
А1А2 = 2a - велика вісь еліпса (проходить через фокуси еліпса)
B1B2 = 2b - мала вісь еліпса (перпендикулярна до великої вісі еліпса та проходить через її центр)
a - велика піввісь еліпса
b - мала піввісь еліпса
O - центр еліпса (точка перетину великої і малої осей еліпса)
Вершини еліпса A1, A2, B1, B2 - точки перетину еліпсу з малою та великою вісями еліпса
Діаметр еліпса - відрізок, який з'єднує дві точки еліпса і проходить через його центр.
Фокальна відстань c - половина довжини відрізку, що з'єднує фокуси еліпса.
Ексцентриситет еліпса e характеризує його витягнутість і визначається відношенням фокальної відстані c до великої піввісі a. Для еліпса ексцентриситет завжди буде 0 < e < 1, для круга e = 0, для параболи e = 1, для гіперболи e > 1.
| e = | c |
| a |
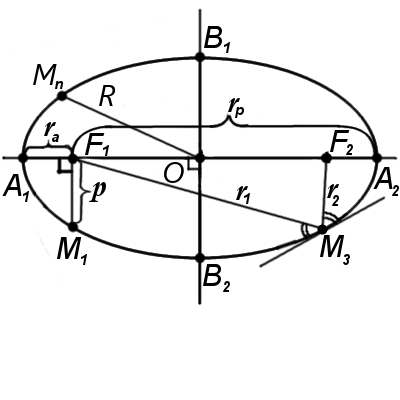
Фокальні радіуси еліпса r1, r2 - відстані від точки на еліпсі до фокусів.
Радіус еліпса R - відрізок, який з'єднує центр еліпса О з точкою на еліпсі.
де e - ексцентриситет еліпса, φ - кут між радіусом та великою віссю A1A2.
| R = | ab | = | b |
| √a2sin2φ + b2cos2φ | √1 - e2cos2φ |
де e - ексцентриситет еліпса, φ - кут між радіусом та великою віссю A1A2.
Фокальний параметр еліпса p - відрізок який виходить з фокусу еліпса та перпендикулярний великій піввісі:
| p = | b2 |
| a |
Коефіцієнт стиску еліпса (еліптичність) k - відношення довжини малої піввісі до великої піввісі. Так як мала піввісь еліпса завжди менша великої, то k < 1, для круга k = 1:
де e - ексцентриситет.
| k = | b |
| a |
k = √1 - e2
де e - ексцентриситет.
Стисненням еліпса (1 - k ) - величина, яка дорівнює різниці між одиницею та еліптичністю:
| 1 - k = | a - b |
| a |
Директриси еліпса - дві прямі перпендикулярні фокальній вісі еліпса, які перетинають її на відстані a e p e
Основні властивості еліпса
1. Кут між дотичною до еліпса і фокальним радіусом r1 дорівнює куту між дотичною і фокальним радіусом r2 (Рис. 2, точка М3).
2. Рівняння дотичної до еліпсу в точці М з координатами (xM, yM):
| 1 = | xxM | + | yyM |
| a2 | b2 |
3. Якщо еліпс перетинається двома паралельними прямими, то відрізок, що сполучає середини відрізків утворених при перетині прямих і еліпса, завжди буде проходити через центр еліпса. (Ця властивість дає можливість за допомогою циркуля і лінійки побудовою отримати центр еліпса.)
4. Еволютою еліпса є астероїда, що витягнута вздовж короткої вісі.
5. Якщо вписати еліпс з фокусами F1 та F2 у трикутник ∆ ABC, то буде виконуватись наступне співвідношення:
| 1 = | F1A ∙ F2A | + | F1B ∙ F2B | + | F1C ∙ F2C |
| CA ∙ AB | AB ∙ BC | BC ∙ CA |
Рівняння еліпса
Канонічне рівняння еліпса:
Рівняння описує еліпс у декартовій системі координат. Якщо центр еліпса О знаходиться на початку координат, а велика вісь лежить на абсцисі, то еліпс описується рівнянням:
Якщо центр еліпса О зміщено в точку з координатами (xo, yo), то рівняння
| 1 = | x2 | + | y2 |
| a2 | b2 |
| 1 = | (x - xo)2 | + | (y - yo)2 |
| a2 | b2 |
Параметричне рівняння еліпса:
| { | x = a cos α | де 0 ≦ α < 2π |
| y = b sin α |
Радіус кола вписаного еліпса
Коло, вписане в еліпс дотикається тільки до двох вершин еліпса, B1 та B2. Відповідно, радіус вписаного кола r буде дорівнювати малій піввісі еліпса OB1:
r = b
Радіус кола описаного навколо еліпса
Коло, описане навколо еліпса дотикається до двох вершин еліпса A1 та A2. Відповідно, радіус описаного кола R буде дорівнювати довжині великої піввісі еліпса OA1:
R = a
Площа еліпса
Формула визначення площі еліпса:
S = πab
Площа сегмента еліпса
Формула площі сегмента, що знаходиться по ліву сторону від хорди з координатами (x, y) та (x, -y):
| S = | πab | - | b | ( | x | √ | a2 - x2 + a2 ∙ arcsin | x | ) |
| 2 | a | a |
Периметр еліпса
Знайти точну формулу периметра еліпса L дуже важко. Нижче наведена формула приблизної довжини периметра. Максимальна похибка цієї формули становить близько ~0,63 %:
| L ≈ 4 | πab + (a - b)2 |
| a + b |
Довжина дуги еліпса
Формули визначення довжини дуги еліпса:
1. Параметрична формула визначення довжини дуги еліпса через велику a та малу b піввісі:
| t2 | ||
| l = | ∫ | √a2sin2t + b2cos2t dt |
| t1 |
2. Параметрична формула визначення довжини дуги еліпса через велику піввісь a та ексцентриситет e:
| t2 | ||
| l = | ∫ | √1 - e2cos2t dt, e < 1 |
| t1 |
Формули з геометрії
Трикутник. Формули та властивості трикутника  Квадрат. Формули та властивості квадрату
Квадрат. Формули та властивості квадрату  Прямокутник. Формули та властивості прямокутника
Прямокутник. Формули та властивості прямокутника  Паралелограм. Формули та властивості паралелограма
Паралелограм. Формули та властивості паралелограма  Ромб. Формули та властивості ромба
Ромб. Формули та властивості ромба  Трапеція. Формули та властивості трапеції
Трапеція. Формули та властивості трапеції  - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції
- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції  - Прямокутна трапеція. Формули та властивості прямокутної трапеції
- Прямокутна трапеція. Формули та властивості прямокутної трапеції  Правильний многокутник. Формули і властивості правильного многокутника
Правильний многокутник. Формули і властивості правильного многокутника  Коло, круг, сегмент, сектор. Формули та властивості
Коло, круг, сегмент, сектор. Формули та властивості  Еліпс. Формули та властивості еліпса
Еліпс. Формули та властивості еліпса  Куб. Формули та властивості куба
Куб. Формули та властивості куба  Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості
Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості  Піраміда. Формули та властивості піраміди
Піраміда. Формули та властивості піраміди  Сфера, куля, сегмент та сектор. Формули та властивості
Сфера, куля, сегмент та сектор. Формули та властивості  Циліндр. Формули та властивості циліндра
Циліндр. Формули та властивості циліндра  Конус. Формули та властивості конуса
Конус. Формули та властивості конуса  Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
 Квадрат. Формули та властивості квадрату
Квадрат. Формули та властивості квадрату  Прямокутник. Формули та властивості прямокутника
Прямокутник. Формули та властивості прямокутника  Паралелограм. Формули та властивості паралелограма
Паралелограм. Формули та властивості паралелограма  Ромб. Формули та властивості ромба
Ромб. Формули та властивості ромба  Трапеція. Формули та властивості трапеції
Трапеція. Формули та властивості трапеції  - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції
- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції  - Прямокутна трапеція. Формули та властивості прямокутної трапеції
- Прямокутна трапеція. Формули та властивості прямокутної трапеції  Правильний многокутник. Формули і властивості правильного многокутника
Правильний многокутник. Формули і властивості правильного многокутника  Коло, круг, сегмент, сектор. Формули та властивості
Коло, круг, сегмент, сектор. Формули та властивості  Еліпс. Формули та властивості еліпса
Еліпс. Формули та властивості еліпса  Куб. Формули та властивості куба
Куб. Формули та властивості куба  Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості
Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості  Піраміда. Формули та властивості піраміди
Піраміда. Формули та властивості піраміди  Сфера, куля, сегмент та сектор. Формули та властивості
Сфера, куля, сегмент та сектор. Формули та властивості  Циліндр. Формули та властивості циліндра
Циліндр. Формули та властивості циліндра  Конус. Формули та властивості конуса
Конус. Формули та властивості конуса  Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
