Сфера, куля, сегмент. Формули, ознаки та властивості сфери

Навігація по сторінці: Означення сфери Означення кулі Об'єм кулі Площа поверхні сфери Рівняння сфери Основні властивості сфери та кулі Січна, хорда, січна площина та їх властивості Дотична, дотична площина та їх властивості Сегмент кулі Зріз кулі Сектор кулі Дотичні сфери Концентричні сфери

Означення.

Сфера (поверхня кулі) — це сукупність усіх точок у тривимірному просторі, які знаходяться на однаковій відстані від однієї точки, що називається центром сфери (О).

Сферу можна описати як об'ємну фігуру, що утворюється підчас обертання кола навколо свого діаметру на 180° чи півкола навколо свого діаметру на 360°.

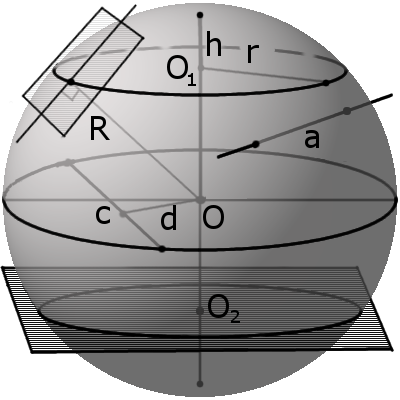
Зображення сфери з позначеннями

Означення.

Куля — це сукупність усіх точок у тривимірному просторі, відстань від яких не перевищує певної відстані від однієї точки, що називається центром кулі (О). (Сукупність усіх точок тривимірного простору обмежених сферою).

Кулю можна описати як об'ємну фігуру, що утворюється обертанням кругу навколо свого діаметру на 180° або напівкругу навколо свого діаметру на 360°.

Означення. Радіус сфери (кулі) (R) - це відстань від центру сфери (кулі) O до будь-якої точки сфери (поверхні кулі).

Означення. Діаметр сфери (кулі) (D) - це відрізок, що з'єднує дві точки сфери (поверхні кулі) та проходить крізь її центр.

Формула. Об'єм кулі:

V =	4	πR³ =	1	πD³
	3		6

Формула. Площа поверхні сфери через радіус або діаметр:

S = 4πR² = πD²

Рівняння сфери

1. Рівняння сфери з радіусом R та центром в початку декартової системи координат:

x² + y² + z² = R²

2. Рівняння сфери з радіусом R та центром в точці з координатами (x₀, y₀, z₀) в декартовій системі координат:

(x - x₀)² + (y - y₀)² + (z - z₀)² = R²

3. Параметричне рівняння сфери з центром в точці (x₀, y₀, z₀):
x = x₀ + R · sin θ · cos φ y = y₀ + R · sin θ · sin φ z = z₀ + R · cos θ
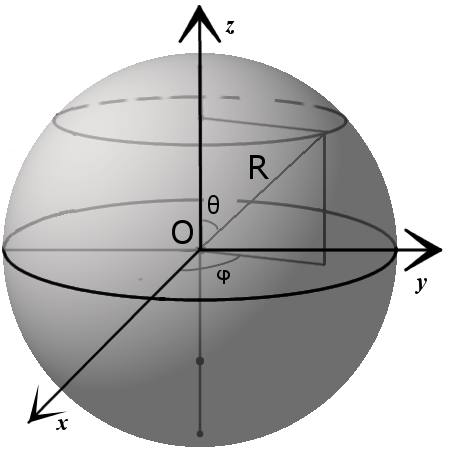
де θ є [0,π], φ ϵ [0,2π].

Означення. Діаметрально протилежними точками називаються будь які дві точки на поверхні кулі (сфері), які з'єднані діаметром.

Основні властивості сфери, кулі

1. Всі точки сфери однаково віддалені від центру.

2. Будь-який переріз сфери площиною є колом.

3. Будь-який переріз кулі площиною є кругом.

4. Куля має найбільший об'єм серед усіх просторових фігур з однаковою площею поверхні.

5. Через будь-які дві діаметрально протилежні точки можна провести безліч великих кіл для сфери або кругів для кулі.

6. Через будь-які дві точки, крім діаметрально протилежних точок, можна провести тільки одне велике коло для сфери або великий круг для кулі.

7. Будь-які два великих круги однієї кулі перетинаються по прямій, що проходить через центр кулі, а кола перетинаються в двох діаметрально протилежних точках.

8. Якщо відстань між центрами будь-яких двох куль менша суми їх радіусів та більша модуля різниці їх радіусів, то такі кулі перетинаються, а в площині перетину утворюється круг.

Січна, хорда, січна площина та їх властивості

Означення. Січна сфери - це пряма, яка перетинає сферу в двох точках. Точки перетину називаються точками протикання поверхні або точками входу та виходу на поверхні.

Означення. Хорда сфери (кулі) - це відрізок, який з'єднує дві точки сфери (поверхні кулі).

Означення. Січна площина - це площина, яка перетинає сферу.

Означення. Діаметральна площина - це січна площина, яка проходить крізь центр сфери або кулі, переріз утворює відповідно велике коло та великий круг. Велике коло та великий круг мають центр, який співпадає з центром сфери (кулі).

Будь-яка хорда, що проходить через центр сфери (кулі) є діаметром.

Хорда є відрізком січної прямої.

Відстань d від центру сфери до січної завжди менша ніж радіус сфери:

d < R

Відстань m між січною площиною та центром сфери завжди менша за радіус R:

m < R

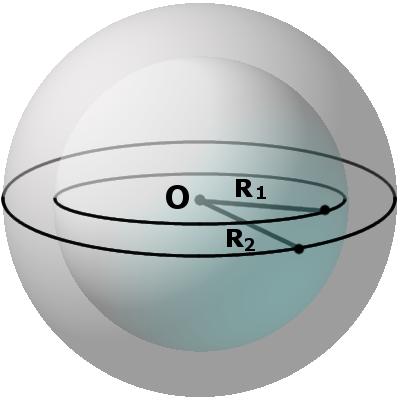
Місцем перерізу січної площини на сфері завжди буде мале коло, а на кулі місцем перерізу буде малий круг. Мале коло і малий круг мають свої центри, які не збігаються з центром сфери (кулі). Радіус такого круга (кола) можна знайти за формулою:

r = √R² - m²,

де R - радіус сфери (кулі), m - відстань від центру кулі до січної площини.

Означення. Півсфера - це половина сфери, яка утворюється при її перетині діаметральною площиною.

Означення. Півкуля - це половина кулі, яка утворюється при її перетині діаметральною площиною.

Дотична до сфери, дотична площина до сфери та їх властивості

Означення. Дотична до сфери - це пряма, що торкається сфери лише в одній точці.

Означення. Дотична площина до сфери - це площина, яка торкається сфери лише в одній точці.

Дотична пряма (площина) завжди перпендикулярна радіусу сфери, проведеному до точки дотику.

Відстань від центру сфери до дотичної прямої (площини) дорівнює радіусу сфери.

Означення. Сегмент кулі - це частина кулі, яка відсікається від кулі площиною. Основою сегменту називають коло, яке утворилося в місці перерізу. Висотою сегменту h називають довжину перпендикуляру, проведеного з середини основи сегменту до поверхні сегменту.

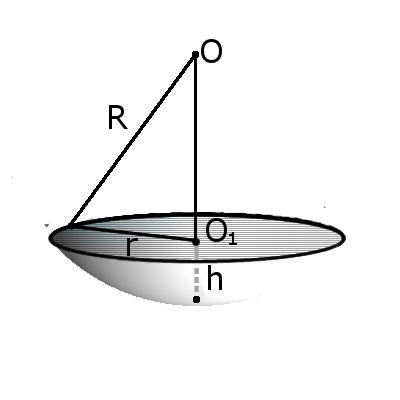
Формула. Площа зовнішньої поверхні сегменту сфери з висотою h через радіус сфери R:

S = 2πRh

Формула. Об'єм сегменту сфери з висотою h через радіус сфери R:

V =	h²π	(3R - h)
	3

Означення. Зріз кулі - це частина кулі, яка утворюється в результаті його перерізу двома паралельними площинами, що знаходиться між ними.

Означення. Сектором називається частина кулі, обмежена сукупністю всіх променів, що виходять з центру кулі О і утворюють коло на його поверхні з радіусом r.

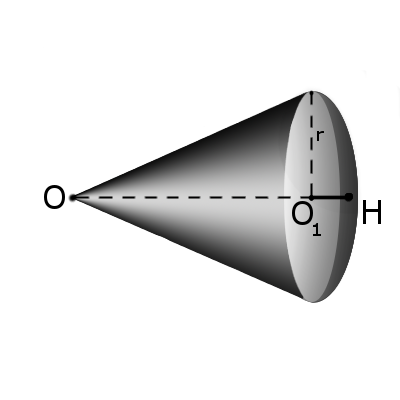
Формула. Площа поверхні сектора S з висотою O₁H (h) через радіус кулі OH (R):

S = πR(2h + √2hR - h²)

Формула. Об'єм сектору V з висотою O₁H (h) через радіус кулі OH (R):

V =	2πR²h
	3

Означення. Дотичними сферами (кулями) називаються будь-які дві сфери (кулі), які мають одну спільну точку дотику. Якщо відстань між центрами більша за суму радіусів, то фігури не торкаються і не перетинаються.