OnlineMSchool
Вивчення математики онлайн.
Вивчайте математику з нами і переконайтесь: "Математика - це просто!"
Реєстрація Увійти Вийти

Прямокутна трапеція. Формули, ознаки та властивості прямокутної трапеції

Навігація по сторінці: Означення прямокутної трапеції Ознаки прямокутної трапеції Основні властивості прямокутної трапеції Сторони прямокутної трапеції Середня лінія прямокутної трапеції
Означення.
Прямокутна трапеція — це трапеція, у якої одна із бокових сторін перпендикулярна основам.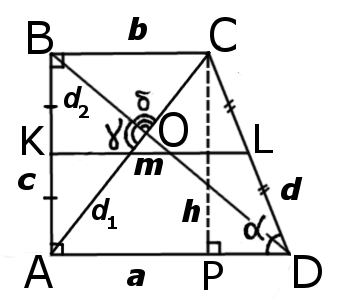
Зображення прямокутної трапеції з позначеннями
Рис.1

Ознаки прямокутної трапеції

Трапеція буде прямокутною, якщо виконується одна із цих умов:
1. В трапеції є два суміжних прямих кута:

∠BAD = 90° и ∠ABC = 90°

2. Одна бокова сторона перпендикулярна основам:

AB ┴ BC, AB ┴ AD


Основні властивості прямокутної трапеції

1. В трапеції є два суміжних прямих кута:

∠BAD = ∠ABC = 90°

2. Одна бокова сторона перпендикулярна основам:

AB ┴ BC ┴ AD

3. Висота рівна меншій боковій стороні:

h = AB


Сторони прямокутної трапеції

Формули довжин сторін прямокутної трапеції:

1. Формули довжин основ через сторони і кут при нижній основі:

a = b + d cos α = b + c ctg α = b + √d 2 - c2

b = a - d cos α = a - c ctg α = a - √d 2 - c2

2. Формули довжин основ через сторони, діагоналі та кут між ними:
a = d1d2 · sin γ - b = d1d2 · sin δ - b
cc
b = d1d2 · sin γ - a = d1d2 · sin δ - a
cc
3. Формули довжин основ трапеції через площу та інші сторони:
a = 2S - b      b = 2S - a
cc
4. Формула бокової сторони через інші сторони та кут при нижній основі:

c = √d 2 - (a - b)2 = (a - b) tg α = d sin α

5. Формули бокової сторони через основи, діагоналі та кут між ними:
c = d1d2 · sin γ = d1d2 · sin δ
a + ba + b
6. Формули бокової сторони через площу, основи та кут при нижній основі:
c = S = 2S
ma + b
d = S = 2S
m sin α(a + b) sin α
7. Формула бокової сторони через інші сторони, висоту та кут при нижній основі:
d = a - b = c = h = √c2 + (a - b)2
cos αsin αsin α

Середня лінія прямокутної трапеції

Формули довжини середньої лінії прямокутної трапеції:

1. Формули середньої лінії через основи, висоту (вона ж рівна стороні d ) та кут α при нижній основі:
m =  a - h · ctg α = b + h · ctg α
22
2. Формули середньої лінії через основи та бокові сторони:
m = a - √d 2 - c2 = b + √d 2 - c2
22

Формули з геометрії Трикутник. Формули та властивості трикутника Квадрат. Формули та властивості квадрату Прямокутник. Формули та властивості прямокутника Паралелограм. Формули та властивості паралелограма Ромб. Формули та властивості ромба Трапеція. Формули та властивості трапеції - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції - Прямокутна трапеція. Формули та властивості прямокутної трапеції Правильний многокутник. Формули і властивості правильного многокутника Коло, круг, сегмент, сектор. Формули та властивості Еліпс. Формули та властивості еліпса Куб. Формули та властивості куба Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду Призма. Формули, ознаки та властивості Піраміда. Формули та властивості піраміди Сфера, куля, сегмент та сектор. Формули та властивості Циліндр. Формули та властивості циліндра Конус. Формули та властивості конуса Формули площі геометричних фігур S Формули периметра геометричних фігур P Формули об'єму геометричних фігур V Формули площі поверхні геометричних фігур S
Всі таблиці і формули

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!

0
Приєднуйтесь до нас