Трикутник. Формули та властивості трикутників.
Типи трикутників
За величиною кутів
- Гострокутний трикутник - всі кути трикутника гострі.

- Тупокутний трикутник - один з кутів трикутника тупий (більше 90°).

- Прямокутний трикутник - один із кутів трикутника прямий (рівний 90°).

За кількістю рівних сторін
- Різносторонній трикутник - всі три сторони не рівні.

- Рівнобедрений трикутник - дві сторони рівні.

- Рівносторонній трикутник або правильний трикутник - всі три сторони рівні.
Вершини, кути та сторони трикутника
Властивості кутів та сторін трикутника
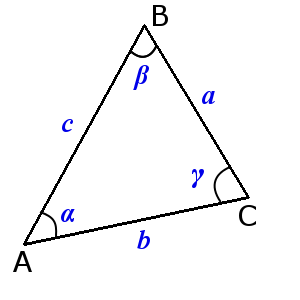
Сума кутів трикутника дорівнює 180°:
α + β + γ = 180°
У трикутнику проти більшої сторони лежить більший кут і навпаки. Проти рівних сторін лежать рівні кути:
якщо α > β, тоді a > b
якщо α = β, тоді a = b
Сума довжин двох будь-яких сторін трикутника більша за довжину сторони, що залишилася:
a + b > c
b + c > a
c + a > b
Теорема синусів
Сторони трикутника пропорційні синусам протилежних кутів.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусів
Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін трикутника мінус подвійний добуток цих сторін на косинус кута між ними.
a2 = b2 + c2 - 2bc·cos α
b2 = a2 + c2 - 2ac·cos β
c2 = a2 + b2 - 2ab·cos γ
Теорема про проекції
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формули для обчислення довжин сторін трикутника
a =
b =
c =
Медіани трикутника
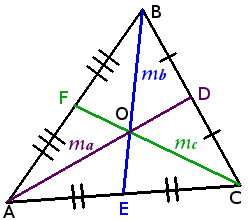
Властивості медіан трикутника:
- Медіани трикутника перетинаються в одній точці. (Точка перетину медіан називається центроїдом)
У точці перетину медіани трикутника поділяються у відношені два до одного (2:1)
AO OD BO OE CO OF 2 1 Медіана трикутника ділить трикутник на дві рівновеликі частини
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
Трикутник ділиться трьома медіанами на шість рівновеликих трикутників.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
- З векторів, що утворюють медіани, можна скласти трикутник.
Формули медіан трикутника
Формули медіан трикутника через сторони
ma =
mb =
mc =
Бісектриси трикутника
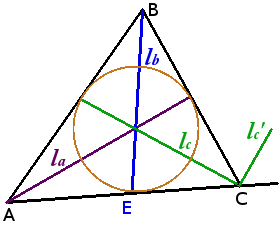
Властивості бісектрис трикутника:
- Бісектриси трикутника перетинаються в одній точці, рівновіддаленій від трьох сторін трикутника, - центрі вписаного кола.
Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні прилеглим сторонам трикутника
AE AB EC BC Кут між бісектрисами внутрішнього і зовнішнього кутів трикутника при одній вершині дорівнює 90°.
Кут між lc та lc' = 90°- Якщо у трикутнику дві бісектриси рівні, то трикутник — равнобедренный.
Формули бісектрис трикутника
Формули бісектрис трикутника через сторони:
la =
lb =
lc =
де p =
Формули бісектрис трикутника через дві сторони і кут:
la =
lb =
lc =
Висоти трикутника
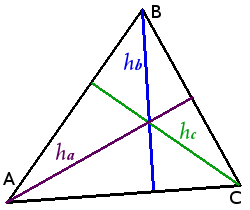
- бути всередині трикутника – для гострокутного трикутника;
- збігатися з його стороною – для катета прямокутного трикутника;
- проходити поза трикутником - для гострих кутів тупокутного трикутника.
Властивості висот трикутника
Формули висот трикутника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
ha =
hb =
hc =
ha =
hb =
hc =
Коло вписане в трикутник
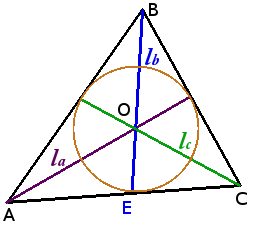
Властивості кола вписаного в трикутник
Формули радіусу кола вписаного в трикутник
r =
r =
Коло описане навколо трикутника
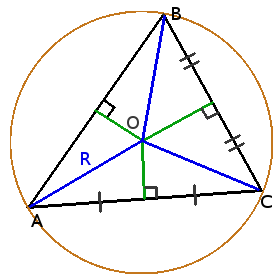
Властивості кола описаного навколо трикутника
Формули радіуса кола описаного навколо трикутника
R =
R =
R =
Зв'язок між вписаним та описании колами трикутника
d2 = R2 - 2Rr
Середня лінія трикутника
Властивості середньої лінії трикутника
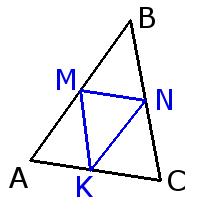
MN =
MN || AC KN || AB KM || BC
S∆MBN =
S∆MAK =
S∆NCK =
∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Периметр трикутника

Периметр трикутника ∆ABC дорівнює сумі довжин його сторін
Формули площі трикутника
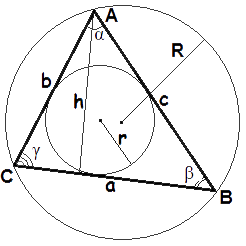
- Формула площі трикутника по стороні та висоті
Площа трикутника дорівнює половині добутку довжини сторони трикутника на довжину проведеної до цієї сторони висотиS =1 2
S =1 2
S =1 2 - Формула площі трикутника за трьома сторонами
Формула Герона
S = √p(p - a)(p - b)(p - c)где p =a + b + c 2 - Формула площі трикутника за двома сторонами та кутом між ними
Площа трикутника дорівнює половині добутка двох його сторін помноженого на синус кута між ними.S =1 2
S =1 2
S =1 2 - Формула площі трикутника по трьох сторонах і радіусу описаного кола
S = a · b · с 4R - Формула площі трикутника по трьох сторонах і радіусу вписаного кола
Площа трикутника дорівнює добутку напівпериметра трикутника на радіус вписаного кола.S = p · r
Рівність трикутників
Ознаки рівності трикутників
Перша ознака рівності трикутників - за двома сторонами та кутом між ними
Якщо дві сторони та кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні.Друга ознака рівності трикутників - за стороною та двом прилеглим кутам
Якщо сторона і два кути, що прилягають до неї одного трикутника, відповідно рівні стороні і двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.Третя ознака рівності трикутників - за трьома сторонам
Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.Подібність трикутників
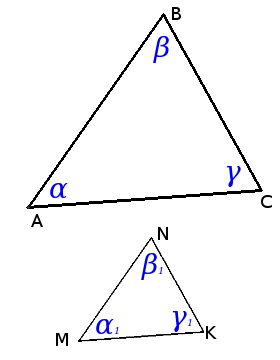
∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и
Ознаки подоби трикутників
Перша ознака подоби трикутників
Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого, то такі трикутники подібні.Друга ознака подібності трикутників
Якщо три сторони одного трикутника пропорційні трьом сторонам іншого, такі трикутники подібні.Третя ознака подоби трикутників
Якщо дві сторони одного трикутника пропорційні двом сторонам іншого, а кути між цими сторонами рівні, то такі трикутники подібні. Квадрат. Формули та властивості квадрату
Квадрат. Формули та властивості квадрату  Прямокутник. Формули та властивості прямокутника
Прямокутник. Формули та властивості прямокутника  Паралелограм. Формули та властивості паралелограма
Паралелограм. Формули та властивості паралелограма  Ромб. Формули та властивості ромба
Ромб. Формули та властивості ромба  Трапеція. Формули та властивості трапеції
Трапеція. Формули та властивості трапеції  - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції
- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції  - Прямокутна трапеція. Формули та властивості прямокутної трапеції
- Прямокутна трапеція. Формули та властивості прямокутної трапеції  Правильний многокутник. Формули і властивості правильного многокутника
Правильний многокутник. Формули і властивості правильного многокутника  Коло, круг, сегмент, сектор. Формули та властивості
Коло, круг, сегмент, сектор. Формули та властивості  Еліпс. Формули та властивості еліпса
Еліпс. Формули та властивості еліпса  Куб. Формули та властивості куба
Куб. Формули та властивості куба  Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості
Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості  Піраміда. Формули та властивості піраміди
Піраміда. Формули та властивості піраміди  Сфера, куля, сегмент та сектор. Формули та властивості
Сфера, куля, сегмент та сектор. Формули та властивості  Циліндр. Формули та властивості циліндра
Циліндр. Формули та властивості циліндра  Конус. Формули та властивості конуса
Конус. Формули та властивості конуса  Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!





