Визначник (детермінант) матриці.

Навігація по сторінці:

Означення визначника (детермінанта) матриці
Властивості визначника матриці
Методи обчислення визначника матриці

Визначник матриці або детермінант матриці - це одна із основних числових характеристик квадратної матриці, що застосовується при розв'язанні багатьох задач.

Означення.

Визначник матриці n×n буде число:

det(A) =	Σ	(-1)^{N(α₁,α₂,...,α_n)}·a_α₁1·a_α₂2·...·a_{α_nn}
	(α₁,α₂,...,α_n)

де (α₁,α₂,...,α_n) - перестановка чисел від 1 до n, N(α₁,α₂,...,α_n) - число інверсій в перестановці, сумування йде по всім можливим перестановкам порядка n.

Позначення.

Визначник матриці A зазвичай позначають det(A), |A|, або ∆(A).

Властивості визначника матриці

Визначник одиничної матриці рівний одиниці:
det(E) = 1
Визначник матриці з двома рівними рядками (стовпцями) рівний нулю.
Визначник матриці з двома пропорційними рядками (стовпцями) рівний нулю.
Визначник матриці, що містить нульовий рядок (стовпчик), рівний нулю.
Визначник матриці рівний нулю, якщо два (або декілька) рядка (стовпця) матриці лінійно залежні.
При транспонуванні значення визначника матриці не змінюється:
det(A) = det(A^T)
Визначник оберненої матриці:
det(A^-1) = det(A)^-1
Визначник матриці не змінюється, якщо до будь-якого його рядка (стовпця) додати інший рядок (стовпчик), помножений на деяке число.
Визначник матриці не змінюється, якщо до будь-якого його рядка (стовпця) додати лінійну комбінацію інших рядків (стовпців).
Якщо поміняти місцями два рядки (стовпця) матриці, то визначник матриці змінить знак.
Загальний множник в рядку (стовпчику) можна винести за знак визначника:
a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... k·a_i1k·a_i2...k·a_in .... a_n1a_n2...a_nn = k· a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... a_i1a_i2...a_in .... a_n1a_n2...a_nn
Якщо квадратна матриця n-того порядка множиться на деяке ненульове число, то визначник отриманої матриці рівний добутку визначника початкової матриці на це число в n-тій степені:
B = k·A => det(B) = kⁿ·det(A)
де A матриця n×n, k - число.
Якщо кожний елемент в будь-якому рядку визначника рівний сумі двох доданків, то початковий визначник рівний сумі двох визначників, в яких замість цього рядка стоїть перший та другий доданок відповідно, а решта рядків співпадають з початковим визначником:
a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... b_i1 + c_i1b_i2 + c_i2...b_in + c_in .... a_n1a_n2...a_nn = a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... b_i1b_i2...b_in .... a_n1a_n2...a_nn + a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... c_i1c_i2...c_in .... a_n1a_n2...a_nn
Визначник верхньої (нижньої) трикутної матриці рівний добутку його діагональних елементів.
Визначник добутку матриць рівний добутку визначників цих матриць:
det(A·B) = det(A)·det(B)

Методи обчислення визначника матриці

Обчислення визначника матриці 1×1

Правило:

Для матриці першого порядка значення визначника рівне значенню елемента цієї матриці:

∆ = |a₁₁| = a₁₁

Обчислення визначника матриці 2×2

Правило:

Для матриці 2×2 значення визначника рівне різниці добутку елементів головної та побічної діагоналей:

∆ =

a₁₁	a₁₂
a₂₁	a₂₂

= a₁₁·a₂₂ - a₁₂·a₂₁

Приклад 1.

Знайти визначник матриці A

A =

	5	7
	-4	1

Розв'язок:

det(A) =

5	7
-4	1

= 5·1 - 7·(-4) = 5 + 28 = 33

Обчислення визначника матриці 3×3

Правило трикутника для обчислення визначника матриці 3-тього порядка

Правило:

Для матриці 3×3 значення визначника рівне сумі добутку елементів головної діагоналі та добутку елементів, що лежать на вершинах трикутника зі стороною, паралельною головній діагоналі, від якої віднімається добуток елементів побічної діагоналі та добутку елементів, що лежать на вершинах трикутника зі стороною, паралельною побічній діагоналі.


+		–

∆ =

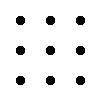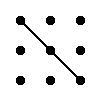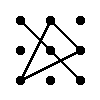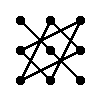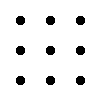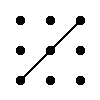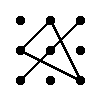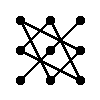a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ - a₁₃·a₂₂·a₃₁ - a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Правило Саррюса для обчислення визначника матриці 3-тього порядка

Правило:

Справа від визначника дописують перших два стовпця визначника, тоді такий детермінант дорівнює сумі добутку елементів на головній діагоналі та на діагоналях, що їй паралельні, та віднімають добуток елементів побічної діагоналі та діагоналей, що їй паралельні:

∆ =

a₁₁	a₁₂	a₁₃	a₁₁	a₁₂
a₂₁	a₂₂	a₂₃	a₂₁	a₂₂
a₃₁	a₃₂	a₃₃	a₃₁	a₃₂

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ - a₁₃·a₂₂·a₃₁ - a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Приклад 2.

Знайти визначник матриці A

A =

5	7	1
-4	1	0
2	0	3

Розв'язок:

det(A) =

5	7	1
-4	1	0
2	0	3

= 5·1·3 + 7·0·2 + 1·(-4)·0 - 1·1·2 - 5·0·0 - 7·(-4)·3 =

= 15 + 0 + 0 - 2 - 0 + 84 = 97

Обчислення визначника матриці довільного розміру

Розклад визначника по рядкам або стовпцям

Правило:

Визначник матриці рівний сумі добутку елементів рядка визначника на їх алгебраїчне доповнення:

	n
det(A) =	Σ	a_ij·A_ij - розклад по i-тому рядку
	j = 1

Правило:

Визначник матриці рівний сумі добутку елементів стовпця визначника на їх алгебраїчне доповнення:

	n
det(A) =	Σ	a_ij·A_ij - розклад по j-тому стовпцю
	i = 1

При розкладі визначника матриці зазвичай вибирають той рядок/стовпчик, в якому максимальна кількість нульових елементів.

Пример 3.

Знайти визначник матриці A

A =

2	4	1
0	2	1
2	1	1

Розв'язок: Обчислимо визначник матриці, розклавши його по першому стовпцю:

det(A) =

2	4	1
0	2	1
2	1	1

= 2·(-1)¹⁺¹·

2	1
1	1

+ 0·(-1)²⁺¹·

4	1
1	1

+ 2·(-1)³⁺¹·

4	1
2	1

= 2·(2·1 - 1·1) + 2·(4·1 - 2·1) = 2·(2 - 1) + 2·(4 - 2) = 2·1 + 2·2 = 2 + 4 = 6

Приклад 4.

Знайти визначник матриці A

A =

2	4	1	1
0	2	0	0
2	1	1	3
4	0	2	3

Розв'язання: Обчислимо визначник матриці, розклавши його по другому рядку (в ньому більше всього нулів):

det(A) =

2	4	1	1
0	2	0	0
2	1	1	3
4	0	2	3

= -0·

4	1	1
1	1	3
0	2	3

+ 2·

2	1	1
2	1	3
4	2	3

- 0·

2	4	1
2	1	3
4	0	3

+ 0·

2	4	1
2	1	1
4	0	2

= 2·(2·1·3 + 1·3·4 + 1·2·2 - 1·1·4 - 2·3·2 - 1·2·3) = 2·(6 +12 + 4 - 4 - 12 - 6) = 2·0 = 0

Зведення визначника до трикутного виду

Правило:

Використовуючи властивості визначника для елементарних перетворень над рядками та стовпцями 8 - 11, визначник зводиться до трикутного виду, і тоді його значення буде рівне добутку елементів головної діагоналі.

Приклад 5.

Знайти визначник матриці A зведенням його до трикутного виду

A =

2	4	1	1
0	2	1	0
2	1	1	3
4	0	2	3

Розв'язок:

det(A) =

2	4	1	1
0	2	1	0
2	1	1	3
4	0	2	3

Спочатку отримаємо нулі в першому стовпчику під головною діагоналлю. Для цього віднімемо від 3-тього рядка 1-ий рядок, а від 4-ого рядка 1-ий рядок, помножений на 2:

det(A) =

2	4	1	1
0	2	1	0
2 - 2	1 - 4	1 - 1	3 - 1
4 - 2·2	0 - 2·4	2 - 2·1	3 - 2·1

2	4	1	1
0	2	1	0
0	-3	0	2
0	-8	0	1

Отримаємо нулі в другому стовпці під головною діагоналлю. Для цього поміняємо місцями 2-ий та 3-тій стовпці:

det(A) = -

2	1	4	1
0	1	2	0
0	0	-3	2
0	0	-8	1

Отримаємо нулі в третьому стовпці під головною діагоналлю. Для цього до 3-го стовпця додамо 4-ий стовпчик, помножений на 8:

det(A) = -

2	1	4 + 8·1	1
0	1	2 + 8·0	0
0	0	-3 + 8·2	2
0	0	-8 + 8·1	1

= -

2	1	12	1
0	1	2	0
0	0	13	2
0	0	0	1

= -2·1·13·1 = -26

Теорема Лапласа

Теорема:

Нехай ∆ - визначник n-ого порядка. Оберемо в ньому довільні k рядків (стовпців), причому k < n. Тоді сума добутків всіх мінорів k-ого порядка, які містяться у вибраних рядках (стовпцях), на їх алгебраїчних доповненнях, рівна визначнику.

Онлайн калькулятори з матрицями.

Вправи з матрицями.

Матриці. Вступ та зміст Матриці: означення та основні поняття Зведення системи лінійних рівнянь до матриці Види матриць Множення матриць на число Додавання та віднімання матриць Множення матриць Транспонування матриць Елементарні перетворення матриць Визначник матриці Мінор та алгебраїчне доповнення матриці Обернена матриця Лінійно залежні та незалежні рядки Ранг матриці

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!