Обернена матриця.

• Означення оберненої матриці
• Властивості оберненої матриці
• Методи обчислення оберненої матриці
  • Обчислення оберненої матриці за допомоги одиничної матриці (Метод Гауса—Жордана)
  • Обчислення оберненої матриці за допомоги союзної(приєднаної) матриці

Обернена матриця A⁻¹ — матриця, добуток якої на початкову матрицю A рівний одиничній матриці E:

A·A^-1 = A^-1·A = E

Обернена матриця існує лише для квадратних матриць, визначник яких не рівний нулю.

●	det(A-1) =  1 det(A)
●	(A·B)-1 = A-1·B-1
●	(A-1)T = (AT)-1
●	(kA)-1 =  A-1 k
●	(A-1)-1 = A

Якщо справа до квадратної матриці дописати одиничну матрицю того ж порядку і за допомоги елементарних перетворень над рядками перетворити отриману матрицю так, щоб початкова матриця стала одиничною, то матриця, отримана за допомоги одиничної, буде оберненою матрицею до початкової.

Якщо при перетвореннях в лівій частині матриці утвориться нульовий рядок (стовпчик), то початкова матриця не матиме оберненої матриці.

Знайти обернену матрицю матриці A

A =		2	4	1
		0	2	1
		2	1	1

Розв'язання: Дописуємо до матриці A справа одиничну матрицю третього порядку:

A|E =		2	4	1	1	0	0		~
		0	2	1	0	1	0
		2	1	1	0	0	1

Перетворимо ліву частину отриманої матриці в одиничну. Для цього від 3-тього рядка віднімемо 1-ий рядок:

~		2	4	1	1	0	0		~
		0	2	1	0	1	0
		2 - 2	1 - 4	1 - 1	0 - 1	0 - 0	1 - 0

~		2	4	1	1	0	0		~
		0	2	1	0	1	0
		0	-3	0	-1	0	1

Третій рядок поділимо на (-3) і поміняємо місцями з другим рядком:

~		2	4	1	1	0	0		~
		0	2	1	0	1	0
		0	1	0	1/3	0	-1/3

~		2	4	1	1	0	0		~
		0	1	0	1/3	0	-1/3
		0	2	1	0	1	0

Віднімемо від 1-го рядка 2-ий рядок, помножений на 4; від 3-го рядка 2-ий рядок, помножений на 2:

~		2 - 4·0	4 - 4·1	1 - 4·0	1 - 4·(1/3)	0 - 4·0	0 - 4·(-1/3)		~
		0	1	0	1/3	0	-1/3
		0 - 2·0	2 - 2·1	1 - 2·0	0 - 2·1/3	1 - 2·0	0 - 2·(-1/3)

~		2	0	1	-1/3	0	4/3		~
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

Віднімемо від 1-ого рядка 3-ій рядок:

~		2 - 0	0 - 0	1 - 1	-1/3 - (-2/3)	0 - 1	4/3 - 2/3		~
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

~		2	0	0	1/3	-1	2/3		~
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

Поділимо 1-ий рядок на 2:

~		1	0	0	1/6	-1/2	1/3
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

Відповідь: A-1 =		1/6	-1/2	1/3
		1/3	0	-1/3
		-2/3	1	2/3

Матриця Ã, елементи якої рівні алгебраїчним доповненням відповідних елементів матриці A, називається союзною матрицею.

A-1 =	1	ÃT
	det(A)

Знайти обернену матрицю матриці A

A =		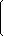2	4	1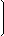
		0	2	1
		2	1	1

Розв'язок: Знайдемо визначник матриці A:

det(A) =	2	4	1	=
	0	2	1
	2	1	1

= 2·2·1 + 4·1·2 + 1·0·1 - 1·2·2 - 2·1·1 - 4·0·1 = 4 + 8 + 0 - 4 - 2 - 0 = 6

Знайдемо алгебраїчне доповнення матриці A:

A11 = (-1)1 + 1·	2	1	= 2·1 - 1·1 = 1
	1	1

A12 = (-1)1 + 2·	0	1	= -(0·1 - 1·2) = 2
	2	1

A13 = (-1)1 + 3·	0	2	= 0·1 - 2·2 = -4
	2	1

A21 = (-1)2 + 1·	4	1	= -(4·1 - 1·1) = -3
	1	1

A22 = (-1)2 + 2·	2	1	= 2·1 - 1·2 = 0
	2	1

A23 = (-1)2 + 3·	2	4	= -(2·1 - 4·2) = 6
	2	1

A31 = (-1)3 + 1·	4	1	= 4·1 - 1·2 = 2
	2	1

A32 = (-1)3 + 2·	2	1	= -(2·1 - 1·0) = -2
	0	1

A33 = (-1)3 + 3·	2	4	= 2·2 - 4·0 = 4
	0	2

Запишемо союзну матрицю:

à =		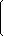1	2	-4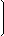
		-3	0	6
		2	-2	4

Знайдемо обернену матрицю:

A-1 =  1 ÃT  =  1 det(A) 6

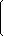1 -3 2 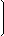2 0 -2 -4 6 4

=

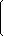1/6 -1/2 1/3 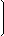1/3 0 -1/3 -2/3 1 2/3

Відповідь: A-1 =		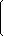1/6	-1/2	1/3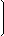
		1/3	0	-1/3
		-2/3	1	2/3