Вектор: означення та основні поняття
Навігація по сторінці:
Означення вектора
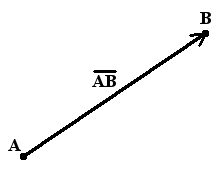
Означення. Вектор - це напрямлений відрізок, тобто відрізок, який має довжину і певний напрямок. Графічно вектори зображуються у вигляді напрямлених відрізків прямої певної довжини. (рис.1)
 |
| рис. 1 |
Позначення вектора
Вектор початком якого є точка А, а кінцем - точка В, позначається AB (рис.1). Також вектори позначають однією маленькою літерою, наприклад a.
Довжина вектора
Означення. Довжина напрямленого відрізка визначає числове значення вектора і називається довжиною вектора або модулем вектора AB.
Для позначення довжини вектора використовують дві вертикальні лінії зліва і справа |AB|.
Нульовий вектор
Означення. Нульовим вектором називається вектор, у якого початкова і кінцева точки співпадають.
Нульовий вектор зазвичай позначають як 0.
Довжина нульового вектора дорівнює нулю.
Колінеарні вектори
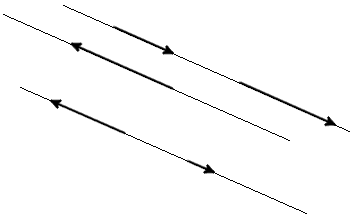
Означення. Вектори, паралельні одній прямій або які лежать на одній прямій називають колінеарними векторами (рис. 2).
 |
| рис. 2 |
Співнаправлені вектори
Означення. Два колінеарних вектора a і b називаються Співнаправленими векторами, якщо їх напрямки співпадають: a↑↑b (рис. 3).
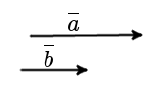 |
| рис. 3 |
Протилежно направлені вектори
Означення. Два колінеарних вектора a і b називаються протилежно направленими векторами, якщо їх напрямок протилежний: a↑↓b (рис. 4).
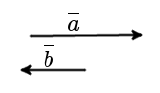 |
| рис. 4 |
Компланарні вектори
Означення. Вектори, паралельні одній площині або які лежать на одній площині називають компланарними векторами. (рис. 5).
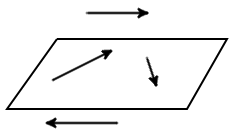 |
| рис. 5 |
Завжди можливо знайти площину паралельну двом довільним векторам, тому будь-які два вектора завжди компланарні.
Рівні вектора
Означення. Вектори a і b називаються рівними, якщо вони лежать на одній прямій або паралельних прямих, їх напрямки співпадають, а довжини рівні (рис. 6).
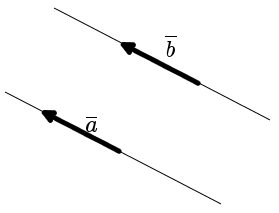 |
| рис. 6 |
Тобто, два вектори рівні, якщо вони колінеарні, співнаправлені та мають рівні довжини:
a = b, якщо a↑↑b і |a| = |b|.
Одиничний вектор
Означення. Одиничним вектором або ортом - називається вектор, довжина якого дорівнює одиниці.
Вектори. Вступ та зміст
Вектор: означення і основні поняття
Знаходження координат вектора заданого координатами його початкової і кінцевої точки
Модуль вектора. Довжина вектора
Напрямні косинуси вектора
Рівність векторів
Ортогональність векторів
Колінеарні вектори
Компланарні вектори
Кут між векторами
Проекція вектора
Додавання і віднімання векторів
Множення вектора на число
Скалярний добуток векторів
Векторний добуток векторів
Мішаний добуток векторів
Лінійно залежні та лінійно незалежні вектори
Розклад вектора за базисом
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
