Формули площі геометричних фігур.
Площа геометричної фігури - числова характеристика геометричної фігури, яка показує розміри цієї фігури (частини поверхні, обмеженої замкнутим контуром даної фігури). Площа вимірюється в квадратних одиницях.
Формули площі плоских фігур:
 Формули площі трикутника
Формули площі трикутника
 Формули площі квадрата
Формули площі квадрата
 Формула площі прямокутника
Формула площі прямокутника
 Формули площі паралелограма
Формули площі паралелограма
 Формули площі ромба
Формули площі ромба
 Формула площі трапеції
Формула площі трапеції
 Формули площі опуклого чотирикутника
Формули площі опуклого чотирикутника
 Формули площі круга
Формули площі круга
 Формула площі еліпса
Формула площі еліпса
 Формули площі трикутника
Формули площі трикутника
 Формули площі квадрата
Формули площі квадрата
 Формула площі прямокутника
Формула площі прямокутника
 Формули площі паралелограма
Формули площі паралелограма
 Формули площі ромба
Формули площі ромба
 Формула площі трапеції
Формула площі трапеції
 Формули площі опуклого чотирикутника
Формули площі опуклого чотирикутника
 Формули площі круга
Формули площі круга
 Формула площі еліпса
Формула площі еліпса
Формули площі трикутника
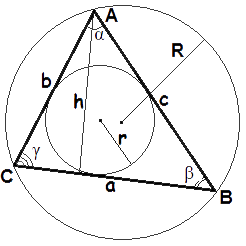
- Формула площі трикутника за стороною та висотою
Площа трикутника дорівнює половині добутку довжини сторони трикутника та довжини проведеної до цієї сторони висотиS = 1 a · h 2 - Формула площі трикутника за трьома сторонами
Формула Герона
S = √p(p - a)(p - b)(p - c) - Формула площі трикутника за двома сторонами і кутом між ними
Площа трикутника дорівнює половині добутку двох його сторін помноженого на синус кута між ними.
S = 1 a · b · sin γ 2 S = 1 a · c · sin β 2 S = 1 b · c · sin α 2 - Формула площі трикутника за трьома сторонам і радіусом описаного кола
S = a · b · с 4R - Формула площі трикутника за трьома сторонами і радіусом вписаного кола
Площа трикутника дорівнює добутку півпериметра трикутника на радіус вписаного кола.
S = p · r
де S - площа трикутника,
a, b, c - довжини сторін трикутника,
h - висота трикутника,
γ - кут між сторонами a и b,
r - радіус вписаного кола,
R - радіус описаного кола,
| p = | a + b + c | - півпериметр трикутника. |
| 2 |
Формули площі квадрата
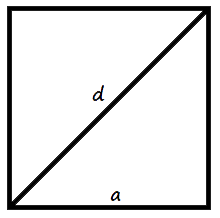
- Формула площі квадрата за довжиною сторони
Площа квадрата дорівнює квадрату довжини його сторони.
S = a2 - Формула площі квадрата за довжиною діагоналіде S - Площа квадрата,
Площа квадрата дорівнює половині квадрата довжини його діагоналі.
S = 1 d2 2
a - довжина сторін квадрата,
d - довжина діагоналей квадрата.
Формула площі прямокутника
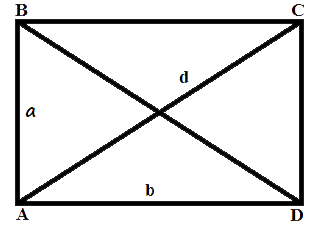
Площа прямокутника дорівнює добутку довжин двох його суміжних сторін
де S - площа прямокутника,S = a · b
a, b - довжини сторін прямокутника.
Формули площі паралелограма
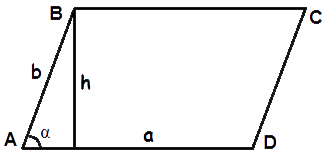
- Формула площі паралелограма за довжиною сторони і висоти
Площа паралелограма дорівнює добутку довжин його сторони і опущеної на цю сторону висоти.
S = a · h - Формула площі паралелограма за двома сторонами і кутом між ними
Площа паралелограма дорівнює добутку довжин його сторін помноженому на синус кута між ними.
S = a · b · sin α - Формула площі паралелограма за двома діагоналями і кутом між ними
Площа паралелограма дорівнює половині добутку довжин його діагоналей, помноженого на синус кута між ними.
S = 1 d1d2 sin γ 2
де S - площа паралелограма,S = 1 d1d2 sin γ 2
a, b - довжини сторін паралелограма,
h - довжина висоти паралелограма,
d1, d2 - довжини діагоналей паралелограма,
α - кут між сторонами паралелограма,
γ - кут між діагоналями паралелограма.
Формули площі ромба
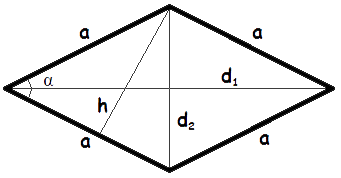
- Формула площі ромба за довжиною сторони і висоти
Площа ромба дорівнює добутку довжин його сторони і опущеної на цю сторону висоти.
S = a · h - Формула площі ромба за довжиною сторони і кутом
Площа ромба дорівнює добутку квадрату довжини його сторони і синуса кута між сторонами ромба.
S = a2 · sin α - Формула площі ромба за довжинами його діагоналейде S - площа ромба,
Площа ромба дорівнює половині добутку довжин його діагоналей.
S = 1 d1 · d2 2
a - довжина сторони ромба,
h - довжина висоти ромба,
α - кут між сторонами ромба,
d1, d2 - довжини діагоналей.
Формула площі трапеції
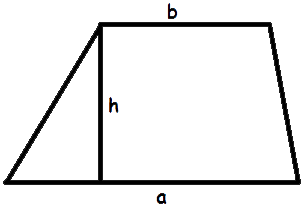
- Формула Герона для трапеції
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a - b| - Формула площі трапеції за довжиною основ і висотиде S - площа трапеції,
Площа трапеції дорівнює добутку півсуми її основ та висоти
S = 1 (a + b) · h 2
a, b - довжини основ трапеції,
c, d - довжини бокових сторін трапеції,
p = a + b + c + d - півпериметр трапеції. 2
Формули площі опуклого чотирикутника
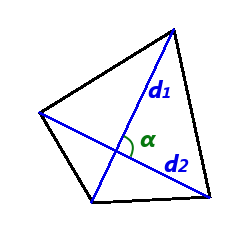
- Формула площі чотирикутника за довжинами діагоналей і куту між нимиде S - площа чотирикутника,
Площа опуклого чотирикутника дорівнює половині добутку йог діагоналей помноженому на синус кута між ними:
S = 1 d1 d2 sin α 2
d1, d2 - довжини діагоналей чотирикутника,
α - кут між діагоналями чотирикутника. - Формула площі описаного чотирикутника (за довжиною периметру і радіусу вписаного кола)
Площа опуклого чотирикутника дорівнює добутку його півпериметру на радіус вписаного кола
S = p · r 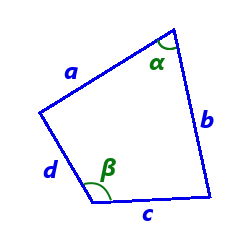 Формула площі чотирикутника за довжиною сторін і значенням протилежних кутівде S - площа чотирикутника,
Формула площі чотирикутника за довжиною сторін і значенням протилежних кутівде S - площа чотирикутника,
S = √(p - a)(p - b)(p - c)(p - d) - abcd cos2θ
a, b, c, d - довжини сторін чотирикутника,
p = a + b + c + d - півпериметр чотирикутника, 2 θ = α + β - півсума двох протилежних кутів чотирикутника. 2 -
Формула площі чотирикутника, навколо якого можна описати коло
S = √(p - a)(p - b)(p - c)(p - d)
Формули площі круга

- Формула площі круга через радіус
Площа круга дорівнює добутку квадрату радіуса та числа пі.
S = π r2 - Формула площі круга через діаметрде S - площа круга,
Площа круга дорівнює чверті добутку квадрата діаметра та числа пі.S = 1 π d2 4
r - довжина радіуса круга,
d - довжина діаметра круга.
Формула площі еліпса
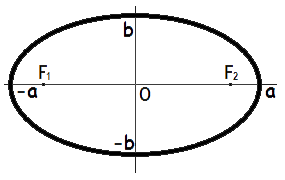
Площа еліпса дорівнює добутку довжин великої і малої піввісі еліпса та число пі.
де S - площа еліпса,
S = π · a · b
a - довжина великої піввісі еліпса,
b - довжина малої піввісі еліпса.
Формули з геометрії
Трикутник. Формули та властивості трикутника  Квадрат. Формули та властивості квадрату
Квадрат. Формули та властивості квадрату  Прямокутник. Формули та властивості прямокутника
Прямокутник. Формули та властивості прямокутника  Паралелограм. Формули та властивості паралелограма
Паралелограм. Формули та властивості паралелограма  Ромб. Формули та властивості ромба
Ромб. Формули та властивості ромба  Трапеція. Формули та властивості трапеції
Трапеція. Формули та властивості трапеції  - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції
- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції  - Прямокутна трапеція. Формули та властивості прямокутної трапеції
- Прямокутна трапеція. Формули та властивості прямокутної трапеції  Правильний многокутник. Формули і властивості правильного многокутника
Правильний многокутник. Формули і властивості правильного многокутника  Коло, круг, сегмент, сектор. Формули та властивості
Коло, круг, сегмент, сектор. Формули та властивості  Еліпс. Формули та властивості еліпса
Еліпс. Формули та властивості еліпса  Куб. Формули та властивості куба
Куб. Формули та властивості куба  Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості
Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості  Піраміда. Формули та властивості піраміди
Піраміда. Формули та властивості піраміди  Сфера, куля, сегмент та сектор. Формули та властивості
Сфера, куля, сегмент та сектор. Формули та властивості  Циліндр. Формули та властивості циліндра
Циліндр. Формули та властивості циліндра  Конус. Формули та властивості конуса
Конус. Формули та властивості конуса  Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
 Квадрат. Формули та властивості квадрату
Квадрат. Формули та властивості квадрату  Прямокутник. Формули та властивості прямокутника
Прямокутник. Формули та властивості прямокутника  Паралелограм. Формули та властивості паралелограма
Паралелограм. Формули та властивості паралелограма  Ромб. Формули та властивості ромба
Ромб. Формули та властивості ромба  Трапеція. Формули та властивості трапеції
Трапеція. Формули та властивості трапеції  - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції
- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції  - Прямокутна трапеція. Формули та властивості прямокутної трапеції
- Прямокутна трапеція. Формули та властивості прямокутної трапеції  Правильний многокутник. Формули і властивості правильного многокутника
Правильний многокутник. Формули і властивості правильного многокутника  Коло, круг, сегмент, сектор. Формули та властивості
Коло, круг, сегмент, сектор. Формули та властивості  Еліпс. Формули та властивості еліпса
Еліпс. Формули та властивості еліпса  Куб. Формули та властивості куба
Куб. Формули та властивості куба  Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості
Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості  Піраміда. Формули та властивості піраміди
Піраміда. Формули та властивості піраміди  Сфера, куля, сегмент та сектор. Формули та властивості
Сфера, куля, сегмент та сектор. Формули та властивості  Циліндр. Формули та властивості циліндра
Циліндр. Формули та властивості циліндра  Конус. Формули та властивості конуса
Конус. Формули та властивості конуса  Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!

