Трапеція. Формули, ознаки та властивості трапеції

Навігація по сторінці: Означення трапеції Складові трапеції Види трапеції Основні властивості трапеції Сторони трапеції Середня лінія трапеції Висота трапеції Діагоналі трапеції Площа трапеції Периметр трапеції Описане коло навколо трапеції Вписане коло в трапецію Інші відрізки трапеції

Означення.

Трапеція — це чотирикутник, у якого дві сторони паралельні, а дві інші сторони не паралельні.

Паралельні сторони називаються основами трапеції, а дві інші боковими сторонами

Також, трапецією називається чотирикутник, у якого одна пара протилежних сторін паралельна, але сторони не рівні між собою.

Елементи трапеції:

Основи трапеції - паралельні сторони
Бокові сторони - дві інші сторони
Середня лінія - відрізок, що з'єднує середини бокових сторін.

Види трапецій:

Рівнобедрена трапеція - трапеція, у якої бокові сторони рівні
Прямокутна трапеція - трапеція, у якої одна із бокових сторін перпендикулярна основам.


Рис.1		Рис.2

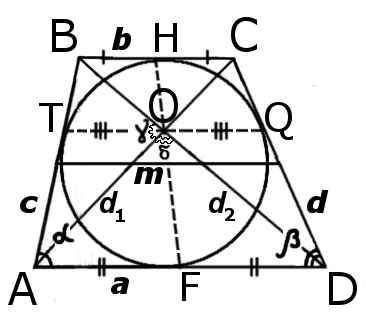
Основні властивості трапеції

1. В трапецію можна вписати коло, якщо сума довжин основи рівна сумі довжин бокових сторін:

AB + CD = BC + AD

2. Середня лінія трапеції розділяє навпіл будь-який відрізок, який з'єднує основи,а також ділить навпіл діагоналі:

AK = KB, AM = MC, BN = ND, CL = LD

3. Середня лінія трапеції паралельна основам і рівна їх півсумі:

m =	a + b
	2

4. Точка перетину діагоналей трапеції і середини основ лежать на одній прямій.

5. В трапеції бокову сторону видно із центра вписаного кола під кутом 90°.

6. Кожна діагональ в точці перетину ділиться на дві частини з таким співвідношенням довжини, як співвідношення між основами:

BC : AD = OC : AO = OB : DO

7. Діагоналі трапеції d₁ і d₂ пов'язані зі сторонами співвідношенням:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеції

Формули визначення довжин сторін трапеції:

1. Формула довжини основ трапеції через середню лінію та іншу основу:

a = 2m - b

b = 2m - a

2. Формули довжин основ через висоту та кути при нижній основі:

a = b + h · (ctg α + ctg β)

b = a - h · (ctg α + ctg β)

3. Формули довжини основ через бокові сторони та кути при нижній основі:

a = b + c·cos α + d·cos β

b = a - c·cos α - d·cos β

4. Формули бокових сторін через висоту та кути при нижній основі:

с =	h	d =	h
	sin α		sin β

Середня лінія трапеції

Означення.

Середня лінія - відрізок, що з'єднує середини бокових сторін трапеції.

Формули визначення довжини середньої лінії трапеції:

1. Формула визначення довжини середньої лінії через довжини основ:

m =	a + b
	2

2. Формула визначення довжин середньої лінії через площу та висоту:

m =	S
	h

Висота трапеції

Формули визначення довжин висоти трапеції:

1. Формула висоти через сторону та прилеглий кут при основі:

h = c·sin α = d·sin β

2. Формула висоти через діагоналі та кути між ними:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
		a + b			a + b

3. Формула висоти через діагоналі, кути між ними та середню лінію:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
		2m			2m

4. Формула висоти трапеції через площу та довжини основ:

h =	2S
	a + b

5. Формула висоти трапеції через площу та довжину середньої лінії:

h =	S
	m

Діагоналі трапеції

Формули визначення довжин діагоналей трапеції:

1. Формули діагоналей за теоремою косинусів:

d₁ = √a² + d² - 2ad·cos β

d₂ = √a² + c² - 2ac·cos α

2. Формули діагоналей через чотири сторони:

d₁ =	√	d ² + ab -	a(d ² - c²)	d₂ =	√	c² + ab -	a(c² - d ²)
			a - b				a - b

3. Формула довжини діагоналей через висоту:

d₁ = √h² + (a - h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a - h · ctg α)² = √h² + (b + h · ctg β)²

4. Формула довжини діагоналей через суму квадратів діагоналей:

d₁ = √c² + d ² + 2ab - d₂²

d₂ = √c² + d ² + 2ab - d₁²

Площа трапеції

Формули визначення площі трапеції:

1. Формула площі через основи та висоту:

S =	(a + b)	· h
	2

2. Формула площі через середню лінію та висоту:

S = m · h

3. Формула площі через діагоналі та кут між ними:

S =	d₁d₂	· sin γ	=	d₁d₂	· sin δ
	2			2

4. Формула площі через чотири сторони:

S =	a + b	√	c² -	(	(a - b)² + c² - d ²	)	²
	2				2(a - b)

5. Формула Герона для трапеції:

S =	a + b	√(p - a)(p - b)(p - a - c)(p - a - d)
	\|a - b\|

де

p =	a + b + c + d	- півпериметр трапеції.
	2

Периметр трапеції

Формула визначення периметра трапеції:

1. Формула периметра через основи:

P = a + b + c + d

Описане коло навколо трапеції

Коло можна описати лише навколо рівнобедреної трапеції!!!

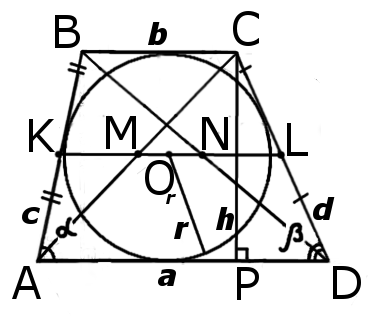
Формула визначення радіуса описаної навколо трапеції кола:

1. Формула радіуса через сторони та діагональ:

R =	a·c·d₁
	4√p(p - a)(p - c)(p - d₁)

де

p =	a + c + d₁
	2

a - більша основа

Вписане коло в трапецію

В трапецію можна вписати коло, якщо сума довжин основ рівна сумі довжин бокових сторін:

a + b = c + d

Формула визначення радіуса вписаного в трапецію кола:

1. Формула радіуса вписаного кола через висоту:

r =	h
	2

Інші відрізки різносторонньої трапеції

Формули визначення довжин відрізків, що проходять через трапецію:

1. Формула визначення довжин відрізків, що проходять через трапецію:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
	2		2		a + b

Формули з геометрії Трикутник. Формули та властивості трикутника

Квадрат. Формули та властивості квадрату

Прямокутник. Формули та властивості прямокутника

Паралелограм. Формули та властивості паралелограма

Ромб. Формули та властивості ромба

Трапеція. Формули та властивості трапеції

- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції

- Прямокутна трапеція. Формули та властивості прямокутної трапеції

Правильний многокутник. Формули і властивості правильного многокутника

Коло, круг, сегмент, сектор. Формули та властивості

Еліпс. Формули та властивості еліпса

Куб. Формули та властивості куба

Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду Призма. Формули, ознаки та властивості

Піраміда. Формули та властивості піраміди

Сфера, куля, сегмент та сектор. Формули та властивості

Циліндр. Формули та властивості циліндра

Конус. Формули та властивості конуса

Формули площі геометричних фігур S Формули периметра геометричних фігур P Формули об'єму геометричних фігур V Формули площі поверхні геометричних фігур S

Всі таблиці і формули

Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.

Підготовка до ДПА по темах.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!