Прямокутник. Формули та властивості прямокутника
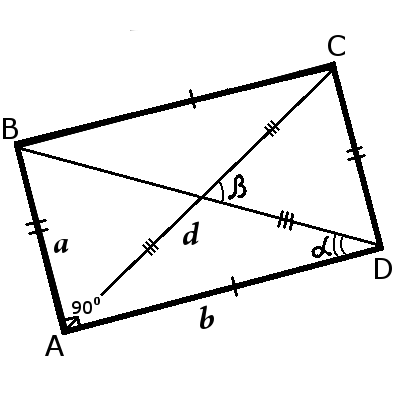
Прямокутники відрізняються між собою тільки співвідношенням довгої сторони до короткої, але всі чотири кути у них прямі, тобто по 90 градусів.
Довшу сторону прямокутника називають довжиною прямокутника, а коротшу - шириною прямокутника.
Сторони прямокутника одночасно є його висотами.
 |
 |
|
| Рис.1 | Рис.2 |
Основні властивості прямокутника
AB = CD, BC = AD
AB||CD, BC||AD
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
AC = BD
2d2 = 2a2 + 2b2
| AO = BO = CO = DO = | d | ||
| 2 |
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
Сторони прямокутника (довжина і ширина прямокутника)
Формули визначення довжин сторін прямокутника
a = √d2 - b2
b = √d2 - a2
| a = | S |
| b |
| b = | S |
| a |
| a = | P - 2b |
| 2 |
| b = | P - 2a |
| 2 |
a = d sinα
b = d cosα
| a = d sin | β |
| 2 |
| b = d cos | β |
| 2 |
Діагональ прямокутника
Формули визначення довжини діагоналі прямокутника
d = √a2 + b2
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
| d = | √P2 - 4Pa + 8a2 | = | √P2 - 4Pb + 8b2 |
| 2 | 2 |
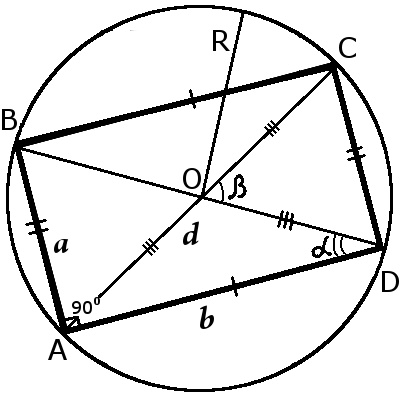
d = 2R
d = Dо
| d = | a |
| sin α |
| d = | b |
| cos α |
d = √2S : sin β
Периметр прямокутника
Формули визначення довжини периметру прямокутника
P = 2a + 2b
P = 2(a + b)
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
P = 2(a + √d2 - a2) = 2(b + √d2 - b2)
P = 2(a + √4R2 - a2) = 2(b + √4R2 - b2)
P = 2(a + √Do2 - a2) = 2(b + √Do2 - b2)
Площа прямокутника
Формули визначення площі прямокутника
S = a · b
| S = | Pa - 2a2 | = | Pb - 2b2 |
| 2 | 2 |
S = a√d2 - a2 = b√d2 - b2
| S = | d2 · sin β |
| 2 |
S = a√4R2 - a2 = b√4R2 - b2
S = a√Do2 - a2 = b√Do2 - b2
Коло, описане навколо прямокутника
Формули визначення радіуса кола, описаного навколо прямокутника
| R = | √a2 + b2 |
| 2 |
| R = | √P2 - 4Pa + 8a2 | = | √P2 - 4Pb + 8b2 |
| 4 | 4 |
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
| R = | d |
| 2 |
| R = | Dо |
| 2 |
| R = | a |
| 2sin α |
| R = | b |
| 2cos α |
| R = | √2S : sin β |
| 2 |
Кут між стороною та діагоналлю прямокутника
Формули визначення кута між стороною та діагоналлю прямокутника
| sin α = | a |
| d |
| cos α = | b |
| d |
| α = | β |
| 2 |
Кут між діагоналями прямокутника
Формули визначення кута між діагоналями прямокутника
β = 2α
| sin β = | 2S |
| d2 |
 Квадрат. Формули та властивості квадрату
Квадрат. Формули та властивості квадрату  Прямокутник. Формули та властивості прямокутника
Прямокутник. Формули та властивості прямокутника  Паралелограм. Формули та властивості паралелограма
Паралелограм. Формули та властивості паралелограма  Ромб. Формули та властивості ромба
Ромб. Формули та властивості ромба  Трапеція. Формули та властивості трапеції
Трапеція. Формули та властивості трапеції  - Рівнобічна трапеція. Формули та властивості рівнобічної трапеції
- Рівнобічна трапеція. Формули та властивості рівнобічної трапеції  - Прямокутна трапеція. Формули та властивості прямокутної трапеції
- Прямокутна трапеція. Формули та властивості прямокутної трапеції  Правильний многокутник. Формули і властивості правильного многокутника
Правильний многокутник. Формули і властивості правильного многокутника  Коло, круг, сегмент, сектор. Формули та властивості
Коло, круг, сегмент, сектор. Формули та властивості  Еліпс. Формули та властивості еліпса
Еліпс. Формули та властивості еліпса  Куб. Формули та властивості куба
Куб. Формули та властивості куба  Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості
Прямокутний паралелепіпед. Формули та властивості прямокутного паралелепіпеду
Призма. Формули, ознаки та властивості  Піраміда. Формули та властивості піраміди
Піраміда. Формули та властивості піраміди  Сфера, куля, сегмент та сектор. Формули та властивості
Сфера, куля, сегмент та сектор. Формули та властивості  Циліндр. Формули та властивості циліндра
Циліндр. Формули та властивості циліндра  Конус. Формули та властивості конуса
Конус. Формули та властивості конуса  Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Формули площі геометричних фігур S
Формули периметра геометричних фігур P
Формули об'єму геометричних фігур V
Формули площі поверхні геометричних фігур S
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
