Ортогональність векторів
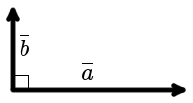 |
| рис. 1 |
Приклади задач на ортогональність векторів
Приклади плоских Приклади задач на ортогональність векторів
Так у випадку плоскої задачі для векторів a = {ax; ay} і b = {bx; by} умова ортогональності запишеться наступним чином:
Розв'язок:
Знайдемо скалярний добуток цих векторів:
a · b = 1 · 2 + 2 · (-1) = 2 - 2 = 0Відповідь: так як скалярний добуток дорівнює нулю, то вектори a і b ортогональні.
Розв'язок:
Знайдемо скалярний добуток цих векторів:
a · b = 3 · 7 + (-1) · 5 = 21 - 5 = 16Відповідь: так як скалярний добуток не дорівнює нулю, то вектори a і b не ортогональні.
Розв'язок:
Знайдемо скалярний добуток цих векторів:
a · b = 2 · n + 4 · 1 = 2n + 42n + 4 = 0
2n = -4
n = -2
Відповідь: вектори a і b будуть ортогональні, якщо n = -2.
Приклади просторових задач на ортогональність векторів
Так у випадку просторової задачі для векторів a = {ax; ay; az} і b = {bx; by; bz} умова ортогональності запишеться наступним чином:
Розв'язок:
Знайдемо скалярний добуток цих векторів:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 - 2 + 0 = 0Відповідь: так як скалярний добуток дорівнює нулю, то вектори a і b ортогональні.
Розв'язок:
Знайдемо скалярний добуток цих векторів:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0Відповідь: так як скалярний добуток дорівнює нулю, то вектори a і b ортогональні.
Розв'язок:
Знайдемо скалярний добуток цих векторів:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 - 8 = 2n - 42n - 4 = 0
2n = 4
n = 2
Відповідь: вектори a і b будуть ортогональні, якщо n = 2.
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
