Компланарність векторів. Умови компланарності векторів
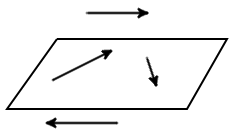 |
| рис. 1 |
Завжди можливо знайти площину паралельну двом довільним векторам, тому будь-які два вектори завжди компланарні.
Умови компланарності векторів
- Для 3-х векторів. Три векторі компланарні якщо їх мішаний добуток дорівнює нулю.
- Для 3-х векторів. Три вектори компланарні якщо вони лінійно залежні.
- Для n векторів. Вектори компланарні якщо серед них не більш ніж два лінійно незалежних векторів.
Приклади задач на компланарність векторів
Розв'язок: Знайдемо мішаний добуток цих векторів
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2
Відповідь: вектори не компланарні так, як їх мішаний добуток не дорівнює нулю.
Розв'язок: Знайдемо мішаний добуток цих векторів
| a · [b × с] = | 1 | 1 | 1 | = |
| 1 | 3 | 1 | ||
| 2 | 2 | 2 |
= 1·2·3 + 1·1·2 + 1·1·2 - 1·2·3 - 1·1·2 - 1·1·2 = 6 + 2 + 2 - 6 - 2 - 2 = 0
Відповідь: вектори компланарні так, як їх мішаний добуток дорівнює нулю.
Розв'язок: Знайдемо кількість лінійно незалежних векторів, для цього запишемо значення векторів в матрицю, і виконаємо над нею елементарні перетворення
| 1 | 1 | 1 | ~ | ||
| 1 | 2 | 0 | |||
| 0 | -1 | 1 | |||
| 3 | 3 | 3 |
від 2-гої стрічки віднімемо 1-шу; від 4-тої стрічки віднімемо 1-шу помножену на 3
| ~ | 1 | 1 | 1 | ~ | 1 | 1 | 1 | ~ | ||||
| 1 - 1 | 2 - 1 | 0 - 1 | 0 | 1 | -1 | |||||||
| 0 | -1 | 1 | 0 | -1 | 1 | |||||||
| 3 - 3 | 3 - 3 | 3 - 3 | 0 | 0 | 0 |
до 3-тьої стрічки додамо 2-гу
| ~ | 1 | 1 | 1 | ~ | 1 | 1 | 1 | ||||
| 0 | 1 | -1 | 0 | 1 | -1 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 | 0 | 0 | ||||||
| 3 - 3 | 3 - 3 | 3 - 3 | 0 | 0 | 0 |
Так як залишилось лише дві ненульові стрічки, то серед приведених векторів лише два лінійно незалежних вектора.
Відповідь: вектори компланарні так, як серед приведених векторів лише два лінійно незалежних вектора.
Інформацію про оновлення та новини сайту дивіться на сторінці у facebook.
Підготовка до ДПА по темах.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
